Cardiovascular Investigations: Open Access Open Access

Introduction

Constructing risk scores for cardiac surgical patients commands a high level of intellectual attention, fueled in part by its multidisciplinary nature and the ever-emerging evidence from cardiac research. The search for an “ideal” model is earnestly pursued as a clinical and methodological undertaking, but the recent developments in statistics and data science have not been appropriately infused into the endeavour. While the celebrated EuroSCORE II, STS and ACEF [1-3] scores continue to serve the needs of the scientific community, it is timey to re-examine the underlying methodological issues and to shed light on the pitfalls of the current practice, which even the most recent reference fails to address [4].

The abovementioned scores are developed with the conventional statistical approach. The underlying model is binary logistic regression (logit), given that the outcome of primary interest is mortality status (survived/dead) at a specific end-point. Constructed with the Binomial distribution and estimated with the maximum-likelihood technique [5], the estimated coefficients (interpreted as odds ratios), which quantify the contribution of their respective predictors with reference to the sign, magnitude and significance, are promised to be “best asymptotically normal”. This means that all statistical inferences, say finding the probability-values and constructing the confidence intervals, could be facilitated with the familiar normal distribution. A forward-selection, backward-elimination or a stepwise procedure is often implemented to search for the “optimal” set of predictors that could best predict the mortality status jointly. The variable selection process also helps to ascertain how a quantitative predictor is associated with mortality (linearly or non-linearly), and to identify its optimum cut-off point with the Receiver Operating Characteristic (ROC) Curve [6]. The goodness-of-fit and calibration of the chosen model is examined with the Hosmer- Lemeshow test (H-L test) [7] and its discriminatory power or predictive accuracy with the area under the ROC (AUC) curve or c-statistics. The finalized equation is translated into a risk score for prediction.

Methods

Thus, there are two integrated tasks in risk-scoring construction: model building and model assessment. The main issue of model building concerns the selection and assessment of the role of individual predictors. In model assessment, the joint performance of the selected predictors is scrutinized, with the score’s predictive accuracy taking the center stage. The advocated practice is to construct a score with the most-updated medical evidence augmented with a sound clinical interpretation, and to let the “data speak for themselves”. An acceptable model is one that could predict the outcome accurately, based on carefullyselected predictors and precisely-estimated coefficients. However, an important feature concerning the role of predictors in the context of cardiac surgery has been overlooked. The predictors in the logit are assumed to be independent. While this facilitates interpretation, it fails to reflect the underlying complexity of the inter-relationships among the predictors in action. As such, it could only provide a partial picture on how each predictor is associated with the mortality status. For example, old age could be associated with arterial stiffness and left ventricular diastolic function [8], which in turn translated into a higher risk of death. The influence of age on death could be direct (measured as an independent predictor) and indirect—manifested through arterial stiffness and left ventricular diastolic function. While age, arterial stiffness and left ventricular diastolic function are baseline predictors, they are not mutually independent in the logical sense. In the context of logit and all conventional regression models, this problem might be highlighted as multicollinearity, which needs to be rectified before the final model is derived. However, the very fact that multicollinearity is often detected suggests that it is a matter of fact that a considerable number of predictors are correlated by nature. It is an undeniable nature of the issue under investigation. The common practice could be to omit of some of these correlated predictors, but this would result in model distortion, lack of fit and loss of information.

A related issue is the application of intraoperative factors in predicting the mortality status. One good example is the cardiopulmonary bypass (CPB) time. The vast majority of Coronary Artery Bypass Graft (CABG) operations are now performed under CPB to take advantage of a motionless and bloodless operative field. However, CPB is not free from side effects and postoperative complications [9], and the extra-corporeal circulation could stimulate an inflammatory response [10], possibly owing to the blood’s exposure to abnormal shearing forces and contact with the artificial surfaces of the bypass circuit [11-13]. It follows that patients’ risk could be amplified with the duration of such exposure. A risk score that ignores the CPB time and depends solely on preoperative factors would thus be inadequate. As such, to better predict the mortality status, the score should factor in intraoperative factors (including aortic cross-clamp time), which could also in turn be analyzed with relevant preoperative factors (e.g., operation-related factors such as urgency of operation). The intraoperative factors are variables that play a dual role in the risk score: as predictors of mortality status and as outcomes of the preoperative factors.

But the conventional logit could not cope with the sequential nature of these predictors. Having the preoperative and intraoperative predictors listed side by side in the logit effectively distorts their natural sequential order. This might result in the detection of multicollinearity and thus generating an erroneous interpretation of the results, in particular how each predictor affects the outcome.

A more complete risk score should involve relevant postoperative outcomes that are expected to affect the mortality status. These include prolonged mechanical ventilation, prolonged intensive care stay, prolonged hospital stay, the needs for re-operations and re-admissions, and the development of complications. Again, these factors must be considered in the risk score according to their sequential nature. The model must be able to consider them as predictors of death (ultimate outcome), and as outcomes to be predicted by relevant preoperative and intraoperative factors. A risk score is only reasonable, useful and comprehensive if it is perioperative in nature, as the occurrence of death could be explained by preoperative, intraoperative and postoperative factors acting individually and jointly, directly and indirectly.

To overcome the problems outlined above and to facilitate a more comprehensive and fruitful analysis involving correlated and sequentially-arranged predictors, the structural equation model (SEM) [14] is recommended. Constructed with an underlying covariance matrix, SEM differs from the conventional regression models in terms of its unique set-up. It could offer more in terms of hypothesis testing and interpretation, and the much needed flexibility in accommodating the preoperative predictors with the intraoperative factors and postoperative outcomes. One does not have to build k separate models with k outcomes, as SEM could accommodate all variables in a single analytical setting and allows the model-builder to specify the sequential ordering of the predictors. It is effectively a system of related equations that enables multiple outcomes of mixed types (qualitative and quantitative) be handled concurrently, and without making unrealistic assumptions (e.g., independence of predictors) required in conventional models. In the event when there are correlated predictors a sub-model is built. As such, the risk prediction model is made up of several sub-models based on the number of intermediate and final outcomes, and each could be interpreted separately.

It is helpful to visualize the proposed modelling strategy in the form of a path diagram (Figure 1), which is an integral part of SEM. It depicts all the data interrelationships involved. For example, PreOP→IntraOp indicates that an analysis is performed for ascertaining the effects of preoperative factors (say creatinine clearance, left ventricular ejection function, PA systolic pressure as in EuroSCORE II) on intraoperative factor (say CPB time). The preoperative factor is in turn predicted with demographics (e.g., age, gender), which are hypothesized to have a direct effect on the intraoperative factors, postoperative outcomes and mortality as well. The preoperative factor constitutes a sub-model within the entire network, so are the intraoperative factors and postoperative outcomes. It is crucial to consider the directions of the arrows. It makes no sense to consider PostOp→IntraOp, as this violates the temporal ordering of the postoperative outcomes and intraoperative factors. Neither is it logical to have PreOp→Demo as it is absurd to test whether prevalence of kidney failure could explain gender. Figure 1 is a simplified path diagram for facilitating discussion, as a box must be specified for a specific predictor in actual practice. In a nutshell, a risk score constructed with gSEM enables one to apply preoperative factors to predict all relevant intraoperative and postoperative outcomes of the cardiac surgery, thus producing a more consolidated, realistic and useful result in prediction.

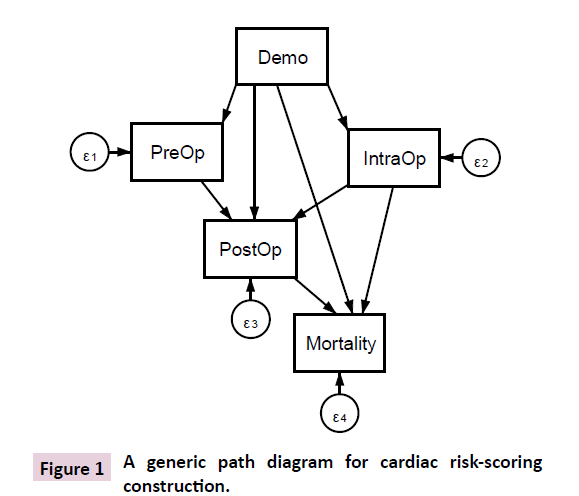
Figure 1: A generic path diagram for cardiac risk-scoring construction.

In passing, note that SEM is not a new endeavour; it is overlooked in medical research but has been successfully applied in cardiovascular research in recent years [15-17]. The latest member of SEM is the generalized SEM (gSEM) [18], which serves to generalize all known parametric models (e.g., generalized linear model, generalized estimating equations, generalized linear mixed model and time-to-event analysis). The specific choice of the underlying probabilistic distributions is determined in accordance with the nature of the outcomes considered in the model. In the case of a binary outcome, the Binomial distribution is appropriate and the generated coefficients are transformed as odds ratios. For counts, an appropriate distribution is Poisson, with the coefficients exponentiated as incidence rate ratios. For continuous outcomes the choice depends on whether they are bell-shaped (Normal), bounded (Beta) or skewed (Inverse Gaussian or Gamma). In time to event analysis the choice could be Weibull and the estimated coefficients are hazard ratios. The gSEM routine and commands are available in popular software packages such as R and Stata. The sample size calculation, however, remains a tricky issue given the complexity but a useful reference is available in literature [19].

With the help of gSEM a more complicated study design could be accommodated. While the well-cited risk scores consider mortality at some end point, it is possible to consider a longitudinal design where the mortality status is monitored in more than one periods, say at 30 days, 31-90 days, 91-365 days and beyond. This would call for the application of a multi-level gSEM [18], which could ascertain the possible change in outcome over the periods explicitly. From a clinical point of view, this could be more informative than considering the mortality status as at some end point.

The issue of variable-selection is discussed next. This is a much trickier issue than the current literature might suggest. It involves not only the selection of specific predictors but how they should be featured in the risk score. For example, LV function, renal dysfunction based on dialysis and creatinine clearance and PA systolic pressure are discretized in EuroSCORE II, and so is serum creatinine in determining the ACEF score. The discretization does not necessarily result in loss of information as the conventional wisdom might suggest [20]. As the ultimate aim is to construct an accurate risk score it makes sense to discretize some quantitative predictors meaningfully, in view of the fact that the risk of death might not be uniform with a unit increase in such predictors [21]. For example, the risk of death might be different for patients in different age groups, as shown in the STS score. Failing to recognize this might reduce the accuracy in prediction. While locating a cut-off with the ROC curve is legitimate, it is not ideal on the very fact that only one cut-off is allowed, even if it is optimal with respect to the sensitivity and specificity. There is no reason to believe that there should be only one cut-off. A more practical approach is not to make any assumption on the number of potential cut-offs but implement a multi-way splitting decision tree, i.e., Chi-square Automatic Interaction Detector (CHAID) [22], to determine what are the cut-off(s). With the help of chi-square test and analysis of variance, CHAID identifies the cut-off(s) by objectively considering how the quantitative predictors should be merged to better predict the outcome of interest. Moreover, CHAID is a multivariate technique that could handle multiple predictors. The model-builder should devote his time and effort to interpret the generated cut-off(s), to make the necessary refinement and to explain the results with justification. It is also worth noting that decision trees are constructed mainly for uncovering relationships among variables and is thus an indispensable tool for variable selection. Once the predictors and their cut-offs/splitting points are identified they are considered in the gSEM for model estimation. In fact, one could apply decision trees for constructing a risk score directly, although they do not possess the statistical properties of logit and gSEM. The product of a decision tree is a rule-based decision in the “if-then” format, rather than a p-value for ascertaining statistical significance.

Conclusion and Discussion

The final issue highlights the pitfalls of logit, H-L test and ROC despite their widespread use. In the context of rare events a logit based on maximum likelihood estimation could underestimate the odds ratios and the probability of event (say death), given that the model is dominated by the overwhelming number of non-events. The degree of bias depends on the number of cases in the less frequent category of outcome under investigation. This is certainly a serious problem as the incidence of death after cardiac surgery is greatly reduced, thanks to advancement in skills and technology. The solution to reduce such bias is to apply the Firth logit [23] and related method [24], but a more careful analysis of how death occurred is desired. It is certainly not a good practice to consider a composite outcome in order to achieve a bigger number, as it masks the sequential nature of death and other postoperative outcomes discussed above. It is a well-known fact that the H-L test is sensitive to the choice of groupings (g) for comparing the actual and expected number of events (say death), and it can be demonstrated that the conclusion concerning the model’s goodness of fit could change drastically with a different g. Despite adhering to the guideline that g should be higher than the number of predictors involved-a much ignored advice in practice-the problem remains. Adding a non-significant predictor could increase the p-value of the test, thereby giving a wrong impression that the model fits the data satisfactorily. Similarly, the ROC curve could also be a misleading measure of logit’s predictive performance, as a poorly-fitted model could possess high discrimination power while a wellfitted model could suffer from poor discrimination [25].

What could one do with these pitfalls then? Bearing in mind that the ultimate aim of a risk score is to predict accurately, it is thus more helpful to report the direct measures: accuracy, sensitivity, specificity and the positive and negative predictive values. Measuring the degree of the separation of events from nonevents, the Kolmogorov-Smirnov chart is a worthy alternative approach for model assessment. Intuitively, a model is evaluated by the ability to separate the events from non-events. A gain or a lift chart may also be reported; these are measures in terms of results obtained with and without the risk prediction model. Several alternative goodness of fit methods that do not require groupings of data could be found in reference [26-28]. Cardiac risk-scoring construction should evolve with a shift from the conventional paradigm of methodology.

References

1. Nashef S, Roques F, Sharples L, Nilsson J, Smith C, et al. (2012) EuroSCORE II. Eur J Cardio-Thorac 41: 734-745.
2. Shahian D, Oâ€Âââ€Å¾Â¢Brien S, Filardo G, Ferraris V, Haan C, et al. (2009) The Society of Thoracic Surgeons 2008 cardia risk models: part 3 valve plus coronary artery bypass grafting surgery. Ann Thorac Surg 88: S43-62.
3. Ranucci M, Castelvecchio S, Menicanti L, Frigiola A, Pelissero G (2009) Risk of assessing mortality risk in elective cardiac operations: age, creatinine, ejection fraction, and the law of parsimony. Circulation 119: 3053-3061.
4. Ranucci M, Di Dedda U, Castelvecchio S, La Rovere M, Menicanti L, et al. (2016) In search of the ideal risk-scoring system for very high-risk cardiac surgical patients: a two-stage approach. J Cardiothorac Surg 11: 13.
5. Nelder J, Wedderburn R (1972) Generalized linear models. J R Stat Soc Ser A-G 135: 370-384.
6. Hanley J, McNeil B (1982) The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 143: 29-36.
7. Hosmer D, Lemeshow S, Sturdivant RX (2013) Applied Logistic Regression, 3rd edn, Wiley, New York.
8. Kim HL, Lim WH, Seo J-B, Chung WY, Kim MA, et al. (2017) Association between arterial stiffness and left ventricular diastolic function in relation to gender and age. Medicine 96: e5783.
9. Murphy G, Angelini G (2004) Side effects of cardiopulmonary bypass: what is the reality? J Card Surg 19: 481-488.
10. Cremer J, Martin M, Redl H, Bahrami S, Abraham C, et al. (1996) Systemic inflammatory response syndrome after cardiac operations. Ann Thorac Surg 61: 1714-1720.
11. Day J, Taylor K (2005) The systemic inflammatory response syndrome and cardiopulmonary bypass. Int J Surg 3: 129-140.
12. Butler J, Rocker G, Westaby S (1993) Inflammatory response to cardiopulmonary bypass. Ann Thorac Surg 1993 55: 552-559.
13. Ohata T, Mitsuno M, Yamamura M, Tanaka H, Kobayashi Y, et al. (2008) Beneficial effects of mini-cardiopulmonary bypass on hemostasis in coronary artery bypass grafting: analysis of inflammatory response and hemodilution. ASAIO J 54: 207-209.
14. Kline R (2011) Principles and practice of structural equation modeling, 3rd edn, The Guilford Press, New York.
15. Kua J, Zhao LP, Kofidis T, Chan SP, Yeo TC, et al. (2015) Sleep apnea is a risk factor for acute kidney injury after coronary artery bypass grafting. Eur J Cardio-thorac 49: 1188-1194.
16. Zhao LP, Kofidis T, Chan SP, Ong TH, Yeo TC, et al. (2015) Sleep apnea and unscheduled readmission in patients undergoing coronary artery bypass surgery. Atherosclerosis 242: 128-134.
17. Zhao LP, You T, Chan SP, Chen JC, Xu WT (2016) Adropin is associated with hyperhomocysteine and coronary atherosclerosis. Exp Ther Med 11: 1065-1070.
18. Rabe-Hesketh S, Skrondal A, Pickels A (2004) Generalized multilevel structural equation modelling. Psychometrika 69: 167-190.
19. Wolf E, Harrington K, Clark S, Miller M (2013) Sample size requirements for structural equation models: an evaluation of power, bias, and solution propriety. Educ Psychol Meas 76: 913-934.
20. Royston P, Altman DG, Sauerbrei W (2006) Dichotomizing continuous predictors in multiple regression: a bad idea. Stat Med 25: 127-141.
21. Kotsiantis S, Kanellopoulos D (2006) Discretization techniques: a recent survey. GESTS Int Trans Comp Sci Eng 32: 47-58.
22. Kass G (1980) An exploratory technique for investigating large quantities of categorical data. Appl Stat 29: 119-127.
23. Firth D (1993) Bias reduction of maximum likelihood estimates. Biometrika 80: 27-38.
24. King G, Zeng L (2001) Logistic regression in rare events data. Polit Anal 9: 137-163.
25. Lobo J, Jimenez-Valverde A, Real R (2008) AUC: a misleading measure of the performance of predictive distribution models. Global Ecol Biogeogr 17: 145-151.
26. Stukel T (1988) Generalized logistic models. J Am Stat Assoc 83: 426-431.
27. Orme C (1990) The small-sample performance of the information-matrix test. J Econometrics 46: 309-331.
28. Tjur T (2009) Coefficients of determination in logistic regression models - a new proposal: the coefficient of determination. Am Stat 63: 366-372.