Keywords
Prime, Strongly prime, Semi prime, Irreducible and strongly irreducible bi-ideals in ternary semi rings.
Introduction
Algebraic structures play a very
outstanding role in mathematics with
classification in multifarious disciplines
such as theoretical physics, computer
sciences, control engineering, information
sciences, coding theory, topological areas
etc. Ternary generalizations of algebraic
structures are the very natural ways for
further development and in depth
comprehension of their basic traits.
Cayley for the first time pioneered
and launched first ternary algebraic
operations in the way back in the 19th
century. Cayley’s ideas expounded and
developed nary generalizations of matrices
and their determinants [9, 14] and general theory
of n-ary algebras [3, 10] and ternary rings [11] (For
physical apllications in Nambu mechanics,
super symmetry, Yang-Baxter equations
etc). Ternary structures and their
generalizations create some hopes because
of their possibility of applications in
physics. A few important physical
applications are listed in [1,2,6,7]. In pursuance
of Lister’s generalizations of ternary rings
introduced in 1971, T. K. Dutta and S. Kar
came up with the notion of ternary
semirings.
T. K. Dutta and S. Kar initiated
prime ideals and prime radical of ternary
semirings in [4]. The same researchers
launched semiprime ideals and irreducible
ideals of ternary semirings in [5]. Furthermore
S. Kar in [8] came up with the notion of quasiideals
and bi-ideals in ternary semi rings.
Similarly, M. Shabir and M. Bano floated
prime bi-ideals in ternary semi groups in [13].
In the opening section of this paper, we
assemble requisite material on prime,
strongly prime and semi prime bi-ternary Γ-
ideals in ternary Γ-semi rings. Deploying the
taxonomic order, we define irreducible and
strongly irreducible bi-ternary Γ-ideals in
ternary Γ-semi rings and specify some classes of ternary Γ-semi rings by the
characteristics of these ternary Γ-ideals.
Preliminaries
Definition 1
Let T and Γ be two additive
commutative semi groups. T is said to be a if there exist a mapping
from T ×Γ× T ×Γ× T to T which maps satisfying
if there exist a mapping
from T ×Γ× T ×Γ× T to T which maps satisfying
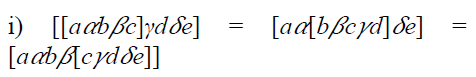 the conditions :
the conditions :
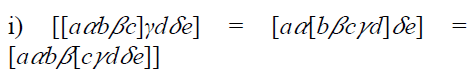
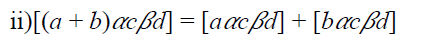
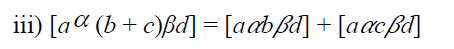
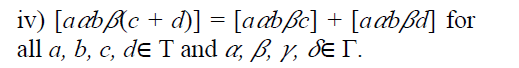
Definition 2
An element 0of a ternary Γ-semiring
T is said to be an absorbing zero of T
provided 0 + x = x = x + 0 and 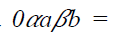
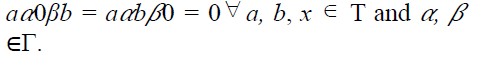
Note 3
Throughout this paper, T will always
denote a ternary Γ-semiring with zero and
unless otherwise stated a ternary Γ-semiring
means a ternary Γ-semiring with zero.
Definition 4
A ternary Γ-semiring T is said to be 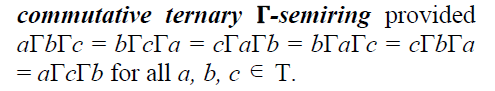
Note 5
For the convenience we write 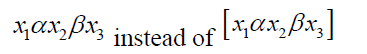
Note 6
Let T be a ternary semiring. If A, B
and C are three subsets of T, we shall denote
the set AΓBΓC = 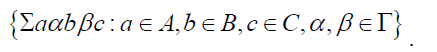
Note 7
Let T be a ternary semiring. If A, B
are two subsets of T, we shall denote the set 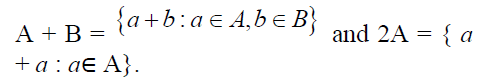
Definition 8
Let T be ternary Γ-semiring. A non
empty subset ‘S’ is said to be a 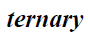
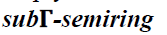 of T if S is an additive
subsemigroup of T and
of T if S is an additive
subsemigroup of T and 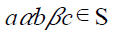 for all
for all 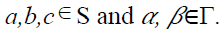
Note 9
A non empty subset S of a ternary Γ-
semiring T is a ternary sub Γ-semiring if and only if 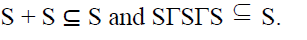
Definition 10
A nonempty subset A of a ternary Γ-
semiring T is said to be 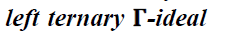
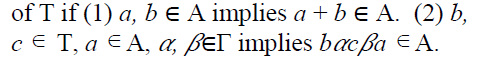
Note 11
A nonempty subset A of a ternary Γ-
semiring T is a left ternary Γ-ideal of T if
and only if A is additive subsemi group of T
and 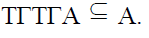
Definition 12
A nonempty subset of a ternary Γ-
semiring T is said to be a 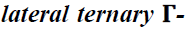
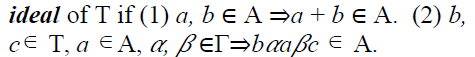
Note 13
A nonempty subset of A of a ternary
Γ-semiring T is a lateral ternary Γ-ideal of T
if and only if A is additive subsemi group of 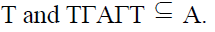
Definition 14
A nonempty subset A of a ternary Γ-
semiring T is a 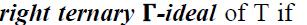

Note 15
A nonempty subset A of a ternary Γ-
semiring T is a right ternary Γ-ideal of T if
and only if A is additive subsemi group of T 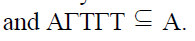
Definition 16
A nonempty subset A of a ternary Γ-
semiring T is said to be ternary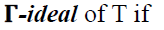
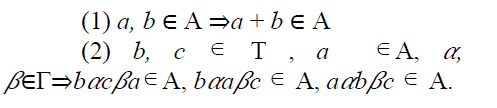
Note 17
A nonempty subset A of a ternary Γ-
semiring T is a ternary Γ-ideal of T if and
only if it is left ternary Γ-ideal, lateral
ternary Γ-ideal and right ternary Γ-ideal of
T.
Definition 18
An element a of a ternary Γ-
semiring. T is said to be regular if there 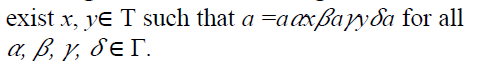
Definition 19
An element a of a ternary Γ-semiring
T is said to be an α-idempotent element
provided 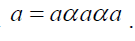
Definition 20
A ternary Γ-semiring T is called α-
idempotent ternary Γ-semiring if every
element of T is α-idempotent.
Definition 21
An element a of a ternary Γ-semiring
T is said to be an 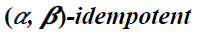 element
provided
element
provided 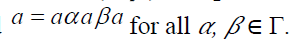
Definition 22
A ternary Γ-subsemiring B of a
ternary Γ-semiring T is called a bi-ternary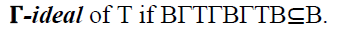
Theorem 22
The intersection of any family of 
Proof
Let 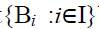 be any family of prime
bi-ternary Γ-ideals of a ternary Γ-semiring T. Let
be any family of prime
bi-ternary Γ-ideals of a ternary Γ-semiring T. Let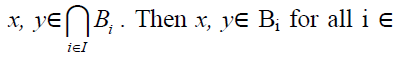 I.As each Bi is a bi-ternary Γ-ideal of T, we
have x + y∈ Bi for all i∈ I implies x +
I.As each Bi is a bi-ternary Γ-ideal of T, we
have x + y∈ Bi for all i∈ I implies x + 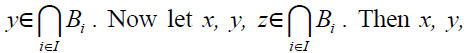 z∈ Bi for all i∈ I.As each Bi is a bi-ternary
Γ-ideal of T, we have
z∈ Bi for all i∈ I.As each Bi is a bi-ternary
Γ-ideal of T, we have 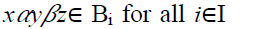 implies
implies 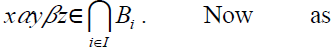
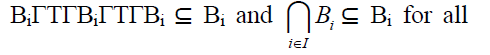
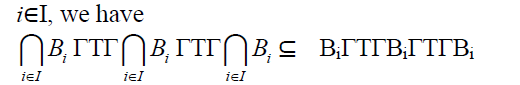
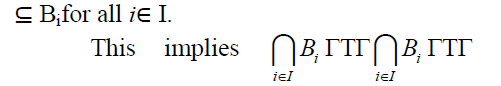
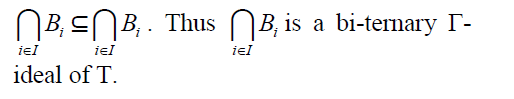
Theorem 23
Every left (right, lateral) ternary
Γ-ideal of a ternary Γ-semiring A is a biternary
Γ-ideal of A.
Theorem 24
If B is a bi-ternary Γ-ideal of a
regular ternary Γ-semiring T and X, Y,
be any non-empty subsets of T, then
B
Corollary 25
If B1,B2,B3 are any bi-ternary Γ-
ideals of a regular ternary Γ-semiring T,
then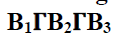 is a bi-ternary Γ-ideal of
T.
is a bi-ternary Γ-ideal of
T.
PRIME, STRONGLY PRIME AND
SEMI PRIME BI-TERNARY
Definition 1
A bi-ternary Γ-ideal B of a ternary Γ-
semiring T is said to be a prime bi-ternary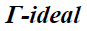 if B1ΓB2ΓB3⊆ B implies B1⊆ B or
B2⊆ B or B3⊆ B for any bi-ternary
Γ-ideals B1,B2,B3 of T.
if B1ΓB2ΓB3⊆ B implies B1⊆ B or
B2⊆ B or B3⊆ B for any bi-ternary
Γ-ideals B1,B2,B3 of T.
Definition 2
A bi-ternary Γ-ideal B of a ternary Γ-
semiring T is said to be a strongly prime bi 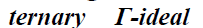 of T if B1ΓB2ΓB3 ∩B2ΓB3ΓB1 ∩B3ΓB1ΓB2⊆ B implies B1⊆ B or B2⊆ B or B3⊆B for any bi-ternary Γ-
ideals B1,B2,B3 of T.
of T if B1ΓB2ΓB3 ∩B2ΓB3ΓB1 ∩B3ΓB1ΓB2⊆ B implies B1⊆ B or B2⊆ B or B3⊆B for any bi-ternary Γ-
ideals B1,B2,B3 of T.
Definition 3
A bi-ternary Γ-ideal B of a ternary Γ-
semiring T is said to be a semi prime bi ternaryΓ-ideal of T if 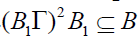 implies
B1⊆B for any bi-ternary Γ-ideal B1 of T.
implies
B1⊆B for any bi-ternary Γ-ideal B1 of T.
Proposition 4
Every strongly prime bi-ternary Γ-
ideal of a ternary Γ-semiring T is a prime
bi-ternary Γ-ideal of T.
Proof
Let B be a strongly prime bi-ternary
Γ-ideal of a ternary Γ-semiring A. Let
B1,B2,B3 be three bi-ternary Γ-ideals of T
such that B1ΓB2ΓB3⊆ B. This implies
B1ΓB2ΓB3 ∩B2ΓB3ΓB1 ∩B3ΓB1ΓB2⊆ B.
Thus B1⊆ B or B2⊆ B or B3⊆ B. Hence B is
a prime bi-ternary Γ-ideal of T.
Theorem 5
Every prime bi-ternary Γ-ideal of
a ternary Γ-semiring T is a semi prime biternary
Γ-ideal of T.
Proof
Let B be a prime bi-ternary Γ-ideal
of a ternary Γ-semiring A. Now let B1 be
any bi-ternary Γ-ideal of T such that 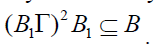 Then B1⊆B.Thus B is a semi
prime bi-ternary Γ-ideal of A.
Then B1⊆B.Thus B is a semi
prime bi-ternary Γ-ideal of A.
Note 6
A prime bi-ternary Γ-ideal of a
ternary Γ-semiring is not necessarily a
strongly prime bi-ternary Γ-ideal and a semi
prime bi-ternary Γ-ideal of a ternary Γ-
semiring is not necessarily a prime biternary
Γ-ideal. This fact is clear from the
following examples:
Example 7
Let A 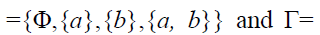
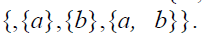 Define addition and
ternary multiplication on T as X+Y = XΔY = (X ∪Y)−(X ∩Y) and (XΓY)ΓZ = X∩Y∩Z
for all X,Y,Z ∈ T. Then T isaternaryΓ- semiring. Bi-ideals of Tare {Φ}, {Φ,{a}}, {Φ,{b}} and {Φ,{a},{b},{a,b}}. Since
(XΓ)2X = X for all X ∈ T, so each bi-ternary
Γ-ideal of T is semi prime. In particular {Φ} is a semi prime bi-ternary Γ-ideal of T but
not a prime bi-ternary Γ-ideal of T, because
{Φ,{a}}Γ{Φ,{b}}Γ{Φ,{a},{b},{a,b}} =
{Φ,{a}}∩{Φ,{b}}∩{Φ,{a},{b},{a, b}}
= {Φ}⊆{Φ}.
Define addition and
ternary multiplication on T as X+Y = XΔY = (X ∪Y)−(X ∩Y) and (XΓY)ΓZ = X∩Y∩Z
for all X,Y,Z ∈ T. Then T isaternaryΓ- semiring. Bi-ideals of Tare {Φ}, {Φ,{a}}, {Φ,{b}} and {Φ,{a},{b},{a,b}}. Since
(XΓ)2X = X for all X ∈ T, so each bi-ternary
Γ-ideal of T is semi prime. In particular {Φ} is a semi prime bi-ternary Γ-ideal of T but
not a prime bi-ternary Γ-ideal of T, because
{Φ,{a}}Γ{Φ,{b}}Γ{Φ,{a},{b},{a,b}} =
{Φ,{a}}∩{Φ,{b}}∩{Φ,{a},{b},{a, b}}
= {Φ}⊆{Φ}.
But none of {Φ,{a}}, {Φ,{b}} and
{Φ,{a},{b},{a,b}} is contained in {Φ}.
Theorem 8
The intersection of any family of
prime bi-ternary Γ-ideals of a ternary Γ-
semiring T is a semi prime bi-ternary Γ-
ideal of T.
Proof
Let{Bi :i∈I}be any family of prime
bi-ternary Γ-ideals of a ternary Γ-semiring
T. We have to show that 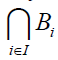 is a
semi
prime bi-ternary Γ-ideal of T. By theorem
2.22,
is a
semi
prime bi-ternary Γ-ideal of T. By theorem
2.22, 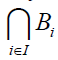 is a bi-ternary Γ-ideal of T. Now
let B be any bi-ternary Γ-ideal of T such that
is a bi-ternary Γ-ideal of T. Now
let B be any bi-ternary Γ-ideal of T such that 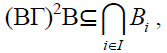 implies BΓBΓB = (BΓ)2B⊆Bi for all i∈I. Thus B ⊆Bi for all
i∈I, because each Bi is a prime bi-ternary Γ-
ideal of T. This implies
implies BΓBΓB = (BΓ)2B⊆Bi for all i∈I. Thus B ⊆Bi for all
i∈I, because each Bi is a prime bi-ternary Γ-
ideal of T. This implies  Hence
Hence 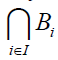 is a semi prime bi-ternary Γ-ideal of T.
is a semi prime bi-ternary Γ-ideal of T.
IRREDUCIBLE AND STRONGLY
IRREDUCIBLE BI-TERNARY
Definition 1
A bi-ternary Γ-ideal B of a ternary Γ-
semiring T is said to be an irreducible bi ternaryΓ-ideal of T if B1∩B2∩B3 = B
implies either B1 = B or B2 = B or B3 = B for
any bi-ternary Γ-ideals B1,B2,B3 of T.
Definition 2
bi-ternary Γ-ideal B of a ternary Γ-
semiring T is said to be a strongly
irreducible bi-ternary Γ-ideal of T if B1∩B2∩B3⊆ B implies either B1⊆ B or B2 ⊆
B or B3 ⊆ B for any bi-ternary Γ-
idealsB1,B2,B3 of T.
Theorem 3
Every strongly irreducible semi
prime bi-ternary 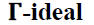 of a ternary
of a ternary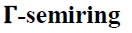 T is a strongly prime biternary
T is a strongly prime biternary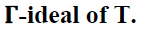
Proof
Let B be a strongly irreducible semi
prime bi-ternary Γ-ideal of a ternary Γ-
semiring T. Let B1,B2,B3 be three bi-ternary
Γ-ideals of T such that
B1ΓB2ΓB3 ∩B2ΓB3ΓB1 ∩B3ΓB1ΓB2⊆
B →(i)
Then we have to show that either
B1⊆B or B2⊆B or B3⊆B. As B1∩B2∩B3⊆
B1,
B1∩B2∩B3⊆ B2 and B1∩B2∩B3⊆ B3 implies [(B1∩B2∩B3)Γ]2(B1∩B2∩B3)⊆B1Γ
B2ΓB3, [(B1∩B2∩B3)Γ]2(B1∩B2∩B3)⊆B2Γ
B3ΓB1 and [(B1∩B2∩B3)Γ]2(B1∩B2∩B3)⊆
B3ΓB1ΓB2.
Thus [(B1∩B2∩B3)Γ]2(B1∩B2∩B3)
⊆B1ΓB2ΓB3 ∩B2ΓB3ΓB1 ∩B3ΓB1ΓB2⊆ B
(by using (i)).
This implies B1∩B2∩B3⊆B, because
B is a semi prime bi-ternary Γ-ideal of T.
Thus B1⊆B or B2⊆B or B3⊆B,
because B is a strongly irreducible bi-ternary
Γ-ideal of T. Hence B is a strongly prime biternary
Γ-ideal of A.
Theorem 4
Let B be a bi-ternary Γ-ideal of a
ternary Γ-semiring T and a∈ T such that
a 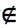 B. Then there exists an irreducible biternary
Γ-ideal I of T such that B ⊆ I and
a
B. Then there exists an irreducible biternary
Γ-ideal I of T such that B ⊆ I and
a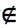 I.
I.
Proof
Let X be the collection of all biternary
Γ-ideals of T which contain B but do not contain a, that is X = {Yi: Yi is a biternary
Γ-ideal of T, B ⊆Yi and a 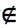 Yi}. Then
X is non-empty as B ∈ X. The collection X
is a partially ordered set under inclusion. If
{Yi: i∈I} is any totally ordered subset
(chain) of X, then
Yi}. Then
X is non-empty as B ∈ X. The collection X
is a partially ordered set under inclusion. If
{Yi: i∈I} is any totally ordered subset
(chain) of X, then 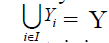 is also a biternary
Γ-ideal of T containing B and a
is also a biternary
Γ-ideal of T containing B and a 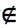 Y.
So Y is an upper bound of {Yi: i∈I}. Thus
every chain in X has an upper bound in X.
Hence by Zorn’s lemma, there exists a
maximal element I (say) in X. This implies
B ⊆I and a
Y.
So Y is an upper bound of {Yi: i∈I}. Thus
every chain in X has an upper bound in X.
Hence by Zorn’s lemma, there exists a
maximal element I (say) in X. This implies
B ⊆I and a 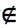 I. Now we show that I is an
irreducible bi-ternary Γ-ideal of T. For this
let C, D and E be three bi-ternary Γ-ideals of
T such that I = C∩D∩E. If C, D and E
properly contain I, then a∈C, a∈D and a∈E.
Thus a∈C∩D∩E = I. Which is a
contradiction to the fact that a
I. Now we show that I is an
irreducible bi-ternary Γ-ideal of T. For this
let C, D and E be three bi-ternary Γ-ideals of
T such that I = C∩D∩E. If C, D and E
properly contain I, then a∈C, a∈D and a∈E.
Thus a∈C∩D∩E = I. Which is a
contradiction to the fact that a 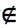 I. So either I
= C or I = D or I = E. Hence I is an
irreducible bi-ternary Γ-ideal of T.
I. So either I
= C or I = D or I = E. Hence I is an
irreducible bi-ternary Γ-ideal of T.
Theorem 5
For a ternary 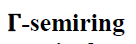 T, the
following assertions are equivalent:
T, the
following assertions are equivalent:
(1) Every bi-ternary 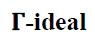 of T is
idempotent.
of T is
idempotent.
(2) B1ΓB2ΓB3∩B2ΓB3ΓB1∩B3ΓB1ΓB2 =
B1∩B2∩B3 for any bi-ternary
(3) Each bi-ternary 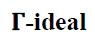 of T is
semiprime.
of T is
semiprime.
(4) Each proper bi-ternary 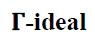 of T is
the intersection of irreducible semiprime
bi-ternary
of T is
the intersection of irreducible semiprime
bi-ternary
Proof
(1) ⇒ (2) Let B1,B2,B3 be any three
bi-ternary Γ-ideals of T. Then B1∩B2∩B3 is
also a bi-ternary Γ-ideal of T, by theorem
22. By hypothesis, we have
B1∩ B2∩B3= [(B1∩B2∩B3)Γ]2(B1∩B2∩B3) =
(B1∩B2∩B3)Γ(B1∩B2∩B3)Γ(B1∩B2∩B3)⊆B 1ΓB2ΓB3.
Similarly
B1∩B2∩B3⊆ B2ΓB3ΓB1 and B1∩B2 ∩B3⊆ B3ΓB1ΓB2.
So B1∩B2∩B3⊆ B1ΓB2ΓB3∩B2ΓB3ΓB1∩B3ΓB1ΓB2.Now B1ΓB2ΓB3,B2ΓB3ΓB1 andB3ΓB1ΓB2, being the products of three
bi-ternary Γ-ideals of T, are bi-ternary Γ-
ideals of T, by Corollary 2.25. Also
B1ΓB2ΓB3∩B2ΓB3ΓB1∩B3ΓB1ΓB2 is a biternary
Γ-ideal of T, by theorem 2.22. Then
by hypothesis
B1ΓB2ΓB3∩B2ΓB3ΓB1∩B3ΓB1ΓB2 = [(B1ΓB2ΓB3∩B2ΓB3ΓB1∩B3ΓB1ΓB2)Γ]2 (B1ΓB2ΓB3∩B2ΓB3ΓB1∩B3ΓB1ΓB2) ⊆(B1Γ
B2ΓB3)Γ(B3ΓB1ΓB2)Γ(B2ΓB3ΓB1)⊆(B1ΓTΓ
T)Γ(TΓB1ΓT)Γ(TΓTΓB1) = B1Γ(TΓTΓT)
ΓB1Γ(TΓTΓT)ΓB1 = B1ΓTΓB1ΓTΓB1⊆ B1
Similarly
B1ΓB2ΓB3∩B2ΓB3ΓB1∩B3ΓB1ΓB2⊆B2 and
B1ΓB2ΓB3∩B2ΓB3ΓB1∩B3ΓB1ΓB2⊆B3.Thus
B1ΓB2ΓB3∩B2ΓB3ΓB1∩B3ΓB1ΓB2⊆B1∩B2 ∩B3.
Hence
B1ΓB2ΓB3∩B2ΓB3ΓB1∩B3ΓB1ΓB2= B1∩B2 ∩B3.
(2) ⇒ (1) Let B be a bi-ternary Γ-
ideal of T.
Then by hypothesis B = B∩B∩B
=BΓBΓB ∩BΓBΓB∩BΓBΓB = BΓBΓB.
(1) ⇒ (3) Let B be a bi-ternary Γ-
ideal of T such that 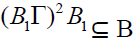 for any biternary
Γ-ideal B1 of T. Then by hypothesis,
we have B1 =
for any biternary
Γ-ideal B1 of T. Then by hypothesis,
we have B1 = 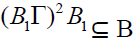 Hence every biternary
Γ-ideal of T is a semiprime biternary Γ-ideal of T
Hence every biternary
Γ-ideal of T is a semiprime biternary Γ-ideal of T
(3) ⇒ (4) Let each bi-ternary Γ-ideal
of T is semiprime. Now let B be a proper biternary
Γ-ideal of T. If 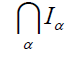 is the intersection of all bi-ternary Γ-ideals of T
containing B, then B ⊆. If this inclusion is
proper, then there exists
is the intersection of all bi-ternary Γ-ideals of T
containing B, then B ⊆. If this inclusion is
proper, then there exists 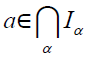 such that
such that 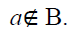
This implies 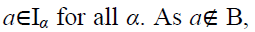 then by Theorem 4.4, there exists an
irreducible bi-ternary Γ-ideal I (say) of T
such that B ⊆ I and
then by Theorem 4.4, there exists an
irreducible bi-ternary Γ-ideal I (say) of T
such that B ⊆ I and 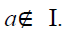 Which is a
contradiction to the fact that
Which is a
contradiction to the fact that  for all α.
So
for all α.
So 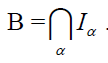 By hypothesis, each bi-ternary
Γ-ideal of T is semiprime. Thus each proper
bi-ternary Γ-ideal of T is the intersection of
irreducible semiprime bi-ternary Γ-ideals of
T which contain it.
By hypothesis, each bi-ternary
Γ-ideal of T is semiprime. Thus each proper
bi-ternary Γ-ideal of T is the intersection of
irreducible semiprime bi-ternary Γ-ideals of
T which contain it.
(4)⇒(1) Let each proper bi-ternary
Γ-ideal of T is the intersection of irreducible
semi prime bi-ternary Γ-ideals of T which
contain it. Now if B is a bi-ternary Γ-ideal of
T, then 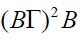 is also a bi-ternary Γ-ideal
of T, by Corollary 2.25. If
is also a bi-ternary Γ-ideal
of T, by Corollary 2.25. If 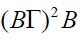 = T
(improper bi-ternary Γ-ideal), then A
= T
(improper bi-ternary Γ-ideal), then A 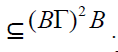 This implies
This implies 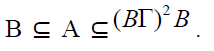
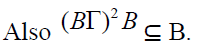
So 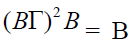 for each bi-ternary
Γ-ideal B of T. Now if
for each bi-ternary
Γ-ideal B of T. Now if 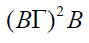 is a proper
bi-ternary Γ-ideal of T, that is
is a proper
bi-ternary Γ-ideal of T, that is 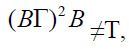 then
then 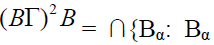 is an irreducible
semiprime bi-ternary Γ-ideal of T such that
is an irreducible
semiprime bi-ternary Γ-ideal of T such that 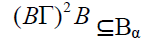 for all α}. This implies B ⊆ Bα
for all α, because each Bα is a semi prime biternary
Γ-ideal of T. Thus B ⊆∩Bα=
for all α}. This implies B ⊆ Bα
for all α, because each Bα is a semi prime biternary
Γ-ideal of T. Thus B ⊆∩Bα= 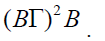
Also 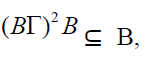 as B is closed
under multiplication. Hence
as B is closed
under multiplication. Hence 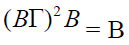 for
each bi-ternary Γ-ideal B of T.
for
each bi-ternary Γ-ideal B of T.
Theorem 6
If each bi-ternary Γ-ideal of a
ternary Γ-semiring T is idempotent then a
bi-ternary Γ-ideal B of T is strongly
irreducible if and only if B is strongly
prime.
Proof
Let B be a strongly irreducible biternary
Γ-ideal of T. Then we have to show
that B is a strongly prime bi-ternary Γ-ideal
of T. For this let B1, B2, B3 be any three biternary
Γ-ideals of T such that B1ΓB2ΓB3 ∩B2ΓB3ΓB1 ∩B3ΓB1ΓB2⊆B. By Theorem
4.5, we have B1 ∩B2 ∩B3 = B1ΓB2ΓB3 ∩B2ΓB3ΓB1 ∩B3ΓB1ΓB2⊆B. But B is a
strongly irreducible bi-ternary Γ-ideal of T.
Thus we have B1⊆ B or B2⊆ B or B3⊆ B.
Hence B is a strongly prime bi-ternary Γ-
ideal of T.
Conversely suppose that B is a
strongly prime bi-ternary Γ-ideal of T. To
show that B is strongly irreducible bi-ternary
Γ-ideal of T, let B1, B2, B3 be any bi-ternary
Γ-ideals of T such that B1 ∩ B2 ∩ B3⊆ B.
By Theorem 4.5, we have B1ΓB2ΓB3 ∩B2ΓB3ΓB1 ∩B3ΓB1ΓB2 = B1 ∩ B2 ∩ B3⊆
B. But B is a strongly prime bi-ternary Γ-
ideal of T, we have B1⊆ B or
B2⊆ B or B3⊆ B. Hence B is a strongly
irreducible bi-ternary Γ-ideal of T.
Next we characterize those ternary
Γ-semi rings in which each bi-ternary Γ-
ideal is strongly prime and also those ternary
Γ-semi rings in which each bi-ternary Γ-
ideal is strongly irreducible.
Theorem 7
Each bi-ternary Γ-ideal of a
ternary Γ-semiring T is strongly prime if
and only if each bi-ternary Γ-ideal of T is Γ-idempotent and the set of bi-ternary Γ-ideal of T is totally ordered by inclusion.
Proof
Suppose that each bi-ternary Γ-ideal
of T is strongly prime. This implies that
each bi-ternary Γ-ideal of T is semiprime.
Thus by Theorem 4.5, each bi- ternary Γ-
ideal of T is idempotent. Now we show that
the set of bi-ternary Γ-ideals of T is totally
ordered by inclusion. For this, let B1, B2 be
two bi-ternary Γ-ideals of T. Then by
Theorem 4.5, we have
B1∩B2 = B1∩B2∩T = B1ΓB2ΓT∩B2Γ
TΓB1∩AΓB1ΓB2, ⇒ B1ΓB2ΓT∩B2ΓTΓB1∩
AΓB1ΓB2⊆B1∩B2.
By hypothesis, B1 and B2 are
strongly prime bi-ternary Γ-ideals of T, so is
B1∩B2. Then B1⊆B1∩B2 or B2⊆B1∩B2 or
T⊆B1∩B2.Thus B1⊆B2 or B2⊆B1.Hence the
set of bi-ternary Γ-ideals of T is totally
ordered by inclusion.
Conversely, assume that each biternary
Γ-ideal of T is Γ-idempotent and the
set of bi-ternary Γ-ideals of T is totally
ordered by inclusion. We have to show that
each bi-ternary Γ-ideal of T is strongly
prime. For this, let B be an arbitrary biternary
Γ-ideal of T and B1, B2, B3 be any
bi-ternary Γ-ideals of T such that B1ΓB2ΓB3 ∩B2ΓB3ΓB1 ∩B3ΓB1ΓB2⊆B. By Theorem
4.5, we have B1∩B2∩B3 = B1ΓB2ΓB3 ∩B2ΓB3ΓB1 ∩B3ΓB1ΓB2⊆B →(i).
Since the set of bi-ternary Γ-ideals of
T is totally ordered by inclusion, so for B1,
B2, B3 we have the following six
possibilities:
(ii) B1⊆B2⊆B3 (iii) B1⊆B3⊆B2
(iv) B2⊆B3⊆B1 (v) B2⊆B1⊆B3
(vi) B3⊆B1⊆B2 (vii) B3⊆B2⊆B1.
In these cases we have
(ii) B1∩B2∩B3 = B1 (iii) B1∩B2∩B3 = B1
(iv) B1∩B2∩B3 = B2 (v) B1∩B2∩B3 = B2
(vi) B1∩B2∩B3 = B3 (vii) B1∩B2∩B3 = B3.
Thus (i) gives, either B1⊆B or B2⊆B
or B3⊆B. Hence B is strongly prime.
Theorem 8
If the set of bi-ternary Γ-ideal of a
ternary Γ-semiring T is totally ordered,
then each bi-ternary Γ-ideal of T is Γ-idempotent if and only if each bi-ternary Γ-ideal of T is prime.
Proof
Suppose each bi-ternary Γ-ideal of T
is Γ-idempotent and B is an arbitrary biternary
Γ-ideal of T and B1, B2, B3 be any
bi-ternary Γ-ideals of T such that
B1ΓB2ΓB3⊆B. As the set of bi-ternary Γ-
ideals of T is totally ordered, then for B1, B2,
B3 we have the following six possibilities:
(i) B1⊆B2⊆B3 (ii) B1⊆B3⊆B2
(iii) B2⊆B3⊆B1 (iv) B2⊆B1⊆B3
(v) B3⊆B1⊆B2 (vi) B3⊆B2⊆B1.
For (i) and (ii), we have 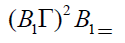 B1ΓB1ΓB1⊆ B1ΓB2ΓB3⊆B, implies B1⊆B,
as B is Γ-idempotent. Similarly for other
possibilities we have B2⊆B or B3⊆B.
B1ΓB1ΓB1⊆ B1ΓB2ΓB3⊆B, implies B1⊆B,
as B is Γ-idempotent. Similarly for other
possibilities we have B2⊆B or B3⊆B.
Conversely, suppose that each biternary
Γ-ideal of T is prime, so is
semiprime, by Theorem 3.5. Thus by
Theorem 4.5, each bi-ternary Γ-ideal of T is
Γ-idempotent.
Theorem 9
If the set of bi-ternary Γ-ideal of a
ternary Γ-semiring T is totally ordered,
then the concepts of primeness and
strongly primeness coincide.
Proof
Let B be a prime bi-ternary Γ-ideal
of T. To show that B is a strongly prime biternary
Γ-ideal of T, let B1, B2, B3 be any biternary
Γ-ideals of T such that
B1ΓB2ΓB3 ∩B2ΓB3ΓB1 ∩B3ΓB1ΓB2⊆B.
As the set of bi-ternary Γ-ideals of
ternary Γ-semiring T is totally ordered, then
for B1, B2, B3 we have the following six
possibilities:
(i) B1⊆B2⊆B3 (ii) B1⊆B3⊆B2
(iii) B2⊆B3⊆B1 (iv) B2⊆B1⊆B3
(v) B3⊆B1⊆B2 (vi) B3⊆B2⊆B1.
For (i) and (ii), we have 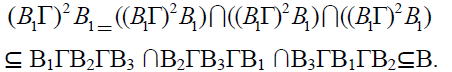
Implies B1⊆ B, as B is a prime biternary
Γ-ideal of T. Similarly for other
possibilities we have B2⊆ B or B3⊆ B. This
shows that B is a strongly prime bi-ternary
Γ-ideal of T. Thus every prime bi-ternary Γ-
ideal of T is a strongly prime bi-ternary Γ-
ideal of T. Now let B be a strongly prime biternary
Γ-ideal of T. To show that B is a
prime bi-ternary Γ-ideal of T, let B1, B2, B3 be any bi-ternary Γ-ideals of T such that
B1ΓB2ΓB3⊆B.Implies B1ΓB2ΓB3 ∩B2ΓB3 ΓB1 ∩B3ΓB1ΓB2⊆B. Implies either B1⊆ B
or B2⊆ B or B3⊆ B, as B is a strongly prime
bi-ternary Γ-ideal of T. This shows that B is
a prime bi-ternary Γ-ideal of T. Thus every
strongly prime bi-ternary Γ-ideal of T is a
prime bi-ternary Γ-ideal of T.
Theorem 10
For a ternary Γ-semiring T, the following assertions are equivalent:
(1) The set of bi-ternary Γ-ideals of T is
totally ordered by set inclusion.
(2) Each bi-ternary Γ-ideal of T is
strongly irreducible.
(3) Each bi-ternary Γ-ideal of T is
irreducible.
Proof
(1) ⇒(2) Let the set of bi-ternary Γ-
ideals of Tis totally ordered by set inclusion.
To show that each bi-ternary Γ-ideal of T is
strongly irreducible, let B be an arbitrary biternary
Γ-ideal of T and B1, B2, B3 be any biternary
Γ-ideals of T such that 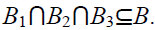 Since the set of bi-ideals of T
is totally ordered by set inclusion, then
Since the set of bi-ideals of T
is totally ordered by set inclusion, then 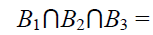 B1 or B2 or B3. Thus either B1⊆
B or B2⊆ B or B3⊆ B. So B is strongly
irreducible. Hence each bi-ternary Γ-ideal of
T is strongly irreducible.
B1 or B2 or B3. Thus either B1⊆
B or B2⊆ B or B3⊆ B. So B is strongly
irreducible. Hence each bi-ternary Γ-ideal of
T is strongly irreducible.
(2) ⇒ (3) Let each bi-ternary Γ-ideal
of T is strongly irreducible. To show that
each bi-ternary Γ-ideal of T is irreducible,
let B be an arbitrary bi-ternary Γ-ideal of T
and B1, B2, B3 be any bi-ternary Γ-ideals of
T such that 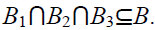 . This implies B ⊆
B1, B ⊆ B2 and B ⊆ B3. On the other hand,
by hypothesis we have B1⊆ B or B2⊆ B or
B3⊆ B. Hence eitherB1 = B or B2 = B or B3 =
B. Thus B is an irreducible bi-ternary Γ-ideal
of T. Hence each bi-ternary Γ-ideal of T is
irreducible.
. This implies B ⊆
B1, B ⊆ B2 and B ⊆ B3. On the other hand,
by hypothesis we have B1⊆ B or B2⊆ B or
B3⊆ B. Hence eitherB1 = B or B2 = B or B3 =
B. Thus B is an irreducible bi-ternary Γ-ideal
of T. Hence each bi-ternary Γ-ideal of T is
irreducible.
(3) ⇒ (1) Let each bi-ternary Γ-ideal
of Tis irreducible. To show that the set of biternary
Γ-ideals of T is totally ordered by set
inclusion, let B1, B2 be any two bi-ternary Γ-
ideals of T. Then by Theorem 22, B1 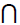 B2 is
also a bi-ternary Γ-ideal of Tand so is
irreducible bi-ternary Γ-ideal of T. Since
B1
B2 is
also a bi-ternary Γ-ideal of Tand so is
irreducible bi-ternary Γ-ideal of T. Since
B1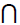 B2
B2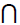 T= B1
T= B1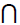 B2, implies B1 = B1
B2, implies B1 = B1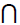 B2 or
B2 = B1
B2 or
B2 = B1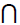 B2 or T= B1
B2 or T= B1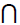 B2, implies either B1⊆
B2 or B2⊆ B1 or B1 = B2 = T. Hence the set
of bi-ternary Γ-ideals of T is totally ordered
by set inclusion.
B2, implies either B1⊆
B2 or B2⊆ B1 or B1 = B2 = T. Hence the set
of bi-ternary Γ-ideals of T is totally ordered
by set inclusion.
Conclusion
In this paper mainly we start the
study of prime Bi-ternary Γ-ideals,
irreducible bi-ternary Γ-ideals in ternary Γ-
semi rings. We characterize them and
results in this paper may apply to many
algebraic structures for further research.
Acknowledgements
This research is supported by the
Department of Mathematics, VSR & NVR
College, Tenali, Guntur (Dt), Andhra
Pradesh, India.
The first and third authors express
their warmest thanks to the University
Grants Commission (UGC), India, for doing this research under Faculty Development
Programme.
The authors would like to thank the experts who have contributed towards preparation and development of the paper and the authors also wish to express their sincere thanks to the referees for the valuable suggestions which lead to an improvement of this paper.
References
- M. Amyari and M. S. Moslehian, Approximate homomorphisms of ternary
semigroups, Letters Math. Physics 77
(2006) 1–9.
- N. Bazunova, A. Borowiec and R. Kerner, Universal differential calculus
on ternary algebras, Letters Math.
Physics 67 (2004) 195–206.
- R. Carlsson, Cohomology of associative triple systems, Proc. Amer. Math. Soc.
60(1976) 1–7.
- T. K. Dutta and S. Kar, on prime ideals and prime radical of ternary semirings, Bull. Cal. Math. Soc. 97(5) (2005) 445–
454.
- T. K. Dutta and S. Kar, Onsemiprime ideals and irreducible ideals of ternary
semirings, Bull. Cal. Math. Soc. 97(5)
(2005) 467–476.
- R. Kerner, The cubic chess coard, class, Quantum Grav. 14 (1997) A203–A225.
- R. Kerner, Ternary algebraic structures and their applications in physics, Univ.
P&M. Curie preprint, Paris (2000) Arxiv
Math-Ph/0011023.
- S. Kar, on quasi-ideals and bi-ideals in ternary semirings, Int. J. Math. Math.Sci.
2005, no. 18, 3015–3023.
- M. Kapranov, I. M. Gelfand and A. Zelevinskii, Discriminants, Resultants
and Multidimensional Determinants,
Birkhauser, Berlin, 1994.
- R. Lawrence, Algebras and Triangle relations, in Topological Methods in
Field Theory, (J. Mickelson and O. Pekonetti, eds.), World Sci., Singapore,
1992, pp. 429–447.
- W. G. Lister, Ternary rings, Trans. Amer. Math. Soc. 154 (1971) 37–55.
- D. Madhuduhana Rao, A. Anjaneyulu and A. Gangadhara Rao, Prime Γ-
radicals in Γ-semi groups, International eJournal of Mathematics and Engineering 138 (2011) 1250-1259.
- M. Shabir and M. Bano, Prime bi-ideals in ternary semigroups, Quasigroups
Related Systems 16 (2008) 239–256.
- N. P. Sokolov, Introduction to the theory of Multidimensional Matrices, Naukova,
Dumka, Kiev, 1972.
- Sajani Lavanya, MadhusudhanaRao and Syam Julius Rajendra., on Quasi-
Ternary Γ-Ideals and Bi-Ternary Γ-
Ideals in Ternary _-Semirings- International Journal of Mathematics and Statistics Invention, Volume 6, Issue
3, September 2015, pp 05-14.
- G. Srinivasa Rao and D. Madhusudhana Rao, Prime Radicals and Completely
Prime Radicals in Ternary Semirings- International Journal of Basic Science and Applied Computing (IJBSAC),
Volume-1 Issue-4, February 2015, pp 1-
5.
- Syam Julius Rajendra. V, Dr. Madhusudhana Rao. D and Sajani
Lavanya. M-On Pure PO-Ternary Γ-
Ideals in Ordered Ternary Γ-Semirings, IOSR Journal of Mathematics (IOSRJM),
Volume 11, Issue 5 Ver. IV (Sep. -
Oct. 2015), PP 05-13.
- Y. Sarala, A. Anjaneyulu and D. Madhusudhana Rao, Prime radicals in
ternary semi groups, International Organization Scientific Research Journal of Mathematics (IOSR-JM) ISSN: 2278-5728 Volume 4, Issue 5
(Jan.-Feb. 2013), pp 43-53.

 if there exist a mapping
from T ×Γ× T ×Γ× T to T which maps satisfying
if there exist a mapping
from T ×Γ× T ×Γ× T to T which maps satisfying
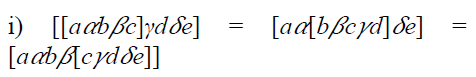 the conditions :
the conditions :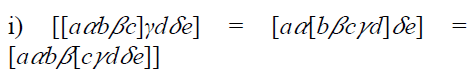
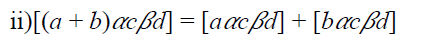
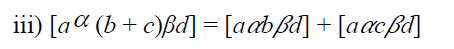
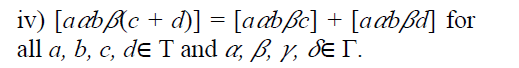
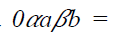
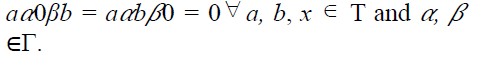
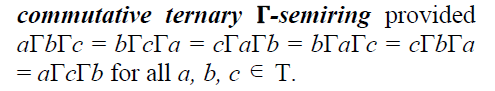
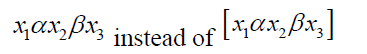
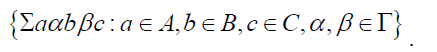
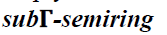 of T if S is an additive
subsemigroup of T and
of T if S is an additive
subsemigroup of T and 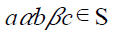 for all
for all 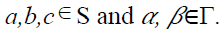
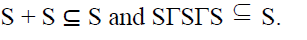
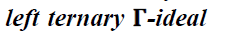
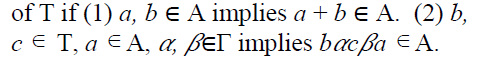
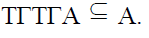
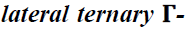
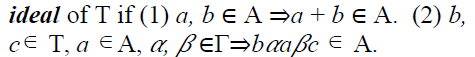
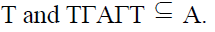
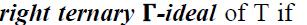

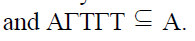
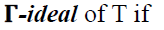
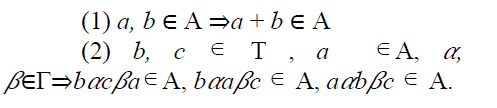
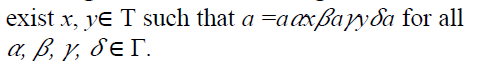
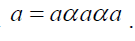
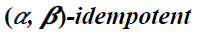 element
provided
element
provided 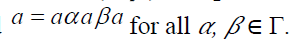
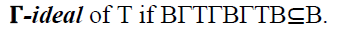

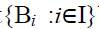 be any family of prime
bi-ternary Γ-ideals of a ternary Γ-semiring T. Let
be any family of prime
bi-ternary Γ-ideals of a ternary Γ-semiring T. Let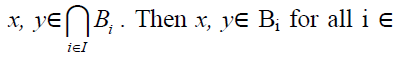 I.As each Bi is a bi-ternary Γ-ideal of T, we
have x + y∈ Bi for all i∈ I implies x +
I.As each Bi is a bi-ternary Γ-ideal of T, we
have x + y∈ Bi for all i∈ I implies x + 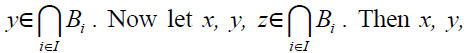 z∈ Bi for all i∈ I.As each Bi is a bi-ternary
Γ-ideal of T, we have
z∈ Bi for all i∈ I.As each Bi is a bi-ternary
Γ-ideal of T, we have 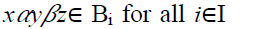 implies
implies 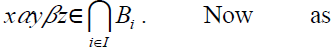
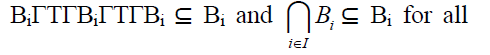
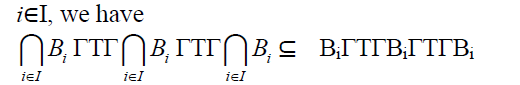
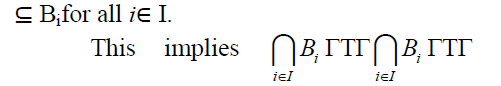
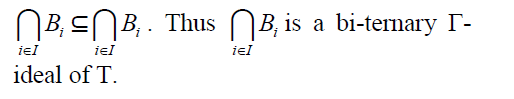
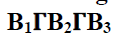 is a bi-ternary Γ-ideal of
T.
is a bi-ternary Γ-ideal of
T.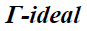 if B1ΓB2ΓB3⊆ B implies B1⊆ B or
B2⊆ B or B3⊆ B for any bi-ternary
Γ-ideals B1,B2,B3 of T.
if B1ΓB2ΓB3⊆ B implies B1⊆ B or
B2⊆ B or B3⊆ B for any bi-ternary
Γ-ideals B1,B2,B3 of T.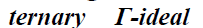 of T if B1ΓB2ΓB3 ∩B2ΓB3ΓB1 ∩B3ΓB1ΓB2⊆ B implies B1⊆ B or B2⊆ B or B3⊆B for any bi-ternary Γ-
ideals B1,B2,B3 of T.
of T if B1ΓB2ΓB3 ∩B2ΓB3ΓB1 ∩B3ΓB1ΓB2⊆ B implies B1⊆ B or B2⊆ B or B3⊆B for any bi-ternary Γ-
ideals B1,B2,B3 of T.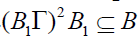 implies
B1⊆B for any bi-ternary Γ-ideal B1 of T.
implies
B1⊆B for any bi-ternary Γ-ideal B1 of T.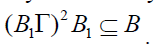 Then B1⊆B.Thus B is a semi
prime bi-ternary Γ-ideal of A.
Then B1⊆B.Thus B is a semi
prime bi-ternary Γ-ideal of A.
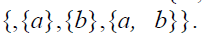 Define addition and
ternary multiplication on T as X+Y = XΔY = (X ∪Y)−(X ∩Y) and (XΓY)ΓZ = X∩Y∩Z
for all X,Y,Z ∈ T. Then T isaternaryΓ- semiring. Bi-ideals of Tare {Φ}, {Φ,{a}}, {Φ,{b}} and {Φ,{a},{b},{a,b}}. Since
(XΓ)2X = X for all X ∈ T, so each bi-ternary
Γ-ideal of T is semi prime. In particular {Φ} is a semi prime bi-ternary Γ-ideal of T but
not a prime bi-ternary Γ-ideal of T, because
{Φ,{a}}Γ{Φ,{b}}Γ{Φ,{a},{b},{a,b}} =
{Φ,{a}}∩{Φ,{b}}∩{Φ,{a},{b},{a, b}}
= {Φ}⊆{Φ}.
Define addition and
ternary multiplication on T as X+Y = XΔY = (X ∪Y)−(X ∩Y) and (XΓY)ΓZ = X∩Y∩Z
for all X,Y,Z ∈ T. Then T isaternaryΓ- semiring. Bi-ideals of Tare {Φ}, {Φ,{a}}, {Φ,{b}} and {Φ,{a},{b},{a,b}}. Since
(XΓ)2X = X for all X ∈ T, so each bi-ternary
Γ-ideal of T is semi prime. In particular {Φ} is a semi prime bi-ternary Γ-ideal of T but
not a prime bi-ternary Γ-ideal of T, because
{Φ,{a}}Γ{Φ,{b}}Γ{Φ,{a},{b},{a,b}} =
{Φ,{a}}∩{Φ,{b}}∩{Φ,{a},{b},{a, b}}
= {Φ}⊆{Φ}.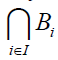 is a
semi
prime bi-ternary Γ-ideal of T. By theorem
2.22,
is a
semi
prime bi-ternary Γ-ideal of T. By theorem
2.22, 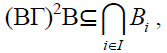 implies BΓBΓB = (BΓ)2B⊆Bi for all i∈I. Thus B ⊆Bi for all
i∈I, because each Bi is a prime bi-ternary Γ-
ideal of T. This implies
implies BΓBΓB = (BΓ)2B⊆Bi for all i∈I. Thus B ⊆Bi for all
i∈I, because each Bi is a prime bi-ternary Γ-
ideal of T. This implies  Hence
Hence 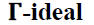 of a ternary
of a ternary T is a strongly prime biternary
T is a strongly prime biternary
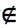 B. Then there exists an irreducible biternary
Γ-ideal I of T such that B ⊆ I and
a
B. Then there exists an irreducible biternary
Γ-ideal I of T such that B ⊆ I and
a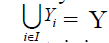 is also a biternary
Γ-ideal of T containing B and a
is also a biternary
Γ-ideal of T containing B and a  T, the
following assertions are equivalent:
T, the
following assertions are equivalent: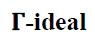 of T is
idempotent.
of T is
idempotent.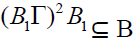 for any biternary
Γ-ideal B1 of T. Then by hypothesis,
we have B1 =
for any biternary
Γ-ideal B1 of T. Then by hypothesis,
we have B1 = 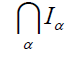 is the intersection of all bi-ternary Γ-ideals of T
containing B, then B ⊆. If this inclusion is
proper, then there exists
is the intersection of all bi-ternary Γ-ideals of T
containing B, then B ⊆. If this inclusion is
proper, then there exists 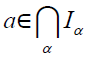 such that
such that 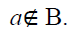
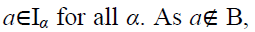 then by Theorem 4.4, there exists an
irreducible bi-ternary Γ-ideal I (say) of T
such that B ⊆ I and
then by Theorem 4.4, there exists an
irreducible bi-ternary Γ-ideal I (say) of T
such that B ⊆ I and 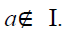 Which is a
contradiction to the fact that
Which is a
contradiction to the fact that  for all α.
So
for all α.
So 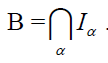 By hypothesis, each bi-ternary
Γ-ideal of T is semiprime. Thus each proper
bi-ternary Γ-ideal of T is the intersection of
irreducible semiprime bi-ternary Γ-ideals of
T which contain it.
By hypothesis, each bi-ternary
Γ-ideal of T is semiprime. Thus each proper
bi-ternary Γ-ideal of T is the intersection of
irreducible semiprime bi-ternary Γ-ideals of
T which contain it.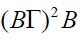 is also a bi-ternary Γ-ideal
of T, by Corollary 2.25. If
is also a bi-ternary Γ-ideal
of T, by Corollary 2.25. If 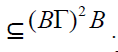 This implies
This implies 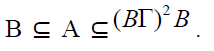
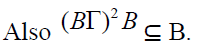
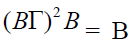 for each bi-ternary
Γ-ideal B of T. Now if
for each bi-ternary
Γ-ideal B of T. Now if 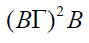 is a proper
bi-ternary Γ-ideal of T, that is
is a proper
bi-ternary Γ-ideal of T, that is 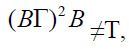 then
then 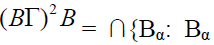 is an irreducible
semiprime bi-ternary Γ-ideal of T such that
is an irreducible
semiprime bi-ternary Γ-ideal of T such that 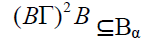 for all α}. This implies B ⊆ Bα
for all α, because each Bα is a semi prime biternary
Γ-ideal of T. Thus B ⊆∩Bα=
for all α}. This implies B ⊆ Bα
for all α, because each Bα is a semi prime biternary
Γ-ideal of T. Thus B ⊆∩Bα= 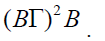
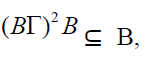 as B is closed
under multiplication. Hence
as B is closed
under multiplication. Hence 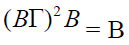 for
each bi-ternary Γ-ideal B of T.
for
each bi-ternary Γ-ideal B of T.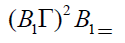 B1ΓB1ΓB1⊆ B1ΓB2ΓB3⊆B, implies B1⊆B,
as B is Γ-idempotent. Similarly for other
possibilities we have B2⊆B or B3⊆B.
B1ΓB1ΓB1⊆ B1ΓB2ΓB3⊆B, implies B1⊆B,
as B is Γ-idempotent. Similarly for other
possibilities we have B2⊆B or B3⊆B.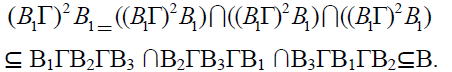
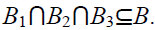 Since the set of bi-ideals of T
is totally ordered by set inclusion, then
Since the set of bi-ideals of T
is totally ordered by set inclusion, then 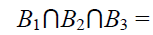 B1 or B2 or B3. Thus either B1⊆
B or B2⊆ B or B3⊆ B. So B is strongly
irreducible. Hence each bi-ternary Γ-ideal of
T is strongly irreducible.
B1 or B2 or B3. Thus either B1⊆
B or B2⊆ B or B3⊆ B. So B is strongly
irreducible. Hence each bi-ternary Γ-ideal of
T is strongly irreducible.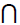 B2 is
also a bi-ternary Γ-ideal of Tand so is
irreducible bi-ternary Γ-ideal of T. Since
B1
B2 is
also a bi-ternary Γ-ideal of Tand so is
irreducible bi-ternary Γ-ideal of T. Since
B1