Editorial - (2017) Volume 18, Issue 2
Alan Kawarai Lefor and Misato Maeno
Department of Surgery, Jichi Medical University, Tochigi Japan
Received January 27th, 2017– Accepted February 10th, 2017
Adenocarcinoma; Pancreas; Pancreatic Neoplasms
The incidence of adenocarcinoma of the pancreas is stable in many countries although it is increasing in some developed countries where it was formerly low. This dreaded disease remains one of the most difficult malignancies to treat and cure. It is often diagnosed in late stage for a wide variety of reasons, and overall about 95% of patients die of their disease within five years. The global incidence is about 8/100,000 people and the incidence in the USA is about 13/100,000. Incidence rates vary about five to seven-fold from countries with the lowest to highest incidences [1].
One of the latest approaches to solving problems in biomedicine is to apply the methods of other established investigative fields. This concept has led to the development of the entire field of Computational Oncology [2]. The idea is to leverage the physical sciences and mathematics to solve problems in oncology, by using a sound mathematical foundation for approaches to oncologic problems. This has led to several approaches to tumor modeling, including descriptive models and mechanistic models.
Mechanistic models have been developed for pancreatic cancer [3]. Investigators have developed a complex model based on signaling pathways in cancer. Specifically, they deal with the pathways for apoptosis, cell cycle arrest and proliferation. This impressive model includes several major signaling pathways, including the Hedgehog, WNT, KRAS, RB-E2F, NFkB, p53, TGF-ß, and apoptosis pathways. The signaling pathways are translated to a Boolean network model, designed with many nodes. The nature of the interactions among the nodes is based on studies of cell function from the laboratory. Each node is a protein or lipid in the signaling pathway. Symbolic Model Checking is then used to verify that the pancreatic cancer cell model satisfies temporal logic properties. The effect of each of the pathways coded can then be evaluated, leading cells to apoptosis, proliferation or cell cycle arrest. This is a very sophisticated model of a single cell, based on known pathways that allow investigators to study the effects of specific signaling pathways on cell activity. It is hoped that this cellular-level insight will be translated into clinically useful therapeutic approaches.
The other type of model used is a descriptive tumor model, which is more likely to be based on patient-based clinical data rather than cellular pathways elucidated in the laboratory. Descriptive tumor models have been used with some success in the field of neuro-oncology, and led to the new discipline of Mathematical Neuro-Oncology [4]. This field uses descriptive tumor models to predict and quantify response to therapy. Advocates of this approach refer to this as precision medicine that uses patient-specific data to tailor therapy. These investigators have developed a model based on the two processes of proliferation and invasion. This mathematical model is defined, in words, as the rate of change of tumor cell density is equal to the net migration of tumor cells plus the net proliferation of tumor cells [4]. In mathematical terms, it is stated as:
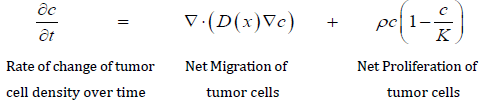
This is a partial differential equation with two parameters: net rate of migration (D) and proliferation (ρ ), both of which are calculated in a patient-specific manner using clinical imaging techniques [4], and is referred to as a Proliferation-Invasion (PI) Model.
The success of the PI model is well documented in the treatment of gliomas. The model was used to simulate surgical resection for 70 patients with glioblastoma and predicted the survival in this group [4]. In addition to predicting tumor growth the PI model has been used to identify patients who might respond to various surgical strategies, predict response to radiation therapy and to connect clinical imaging features and genetic information [5]. While the clinical behavior of glioblastoma is not the same as adenocarcinoma of the pancreas, computational oncology may offer insights into various therapeutic approaches for patients with adenocarcinoma of the pancreas.
Haeno and Michor developed a descriptive model of the growth of tumors, which begins with consideration of tumor cells in three groups, type-0 cells which reside in the primary tumor and are not yet able to metastasize, type-1 cells which can metastasize and type-2 cells which have metastasized and form new lesions [6]. They used this model to derive several analytical approximations, including: (i) the probability of having at least one metastatic site at diagnosis and at autopsy; (ii) the expected number of metastatic sites at diagnosis and at autopsy; and (iii) the expected total number of cells in all metastatic sites at diagnosis and at autopsy [6]. By considering the cells of a tumor in these three groups and having analytic approximations to relate the size of each group, they can study the effects of various changes on the overall cell population. This model also allows the calculation of the effect of drug administration and tumor resection on the number of cells in each group, which can then be used to predict survival. This model predicts that tumor resection effectively prolongs survival when the tumor is large. The effect of the various parameters they use on metastatic rate, timing of the occurrence of metastases and growth of metastases can be demonstrated with this sophisticated model. This is the beginning of detailed descriptive mathematical modeling of tumor growth that can be correlated with a patient’s clinical findings.
These same investigators then applied their descriptive tumor model to patients with adenocarcinoma of the pancreas [7]. In this study, they used data from 228 patients with adenocarcinoma of the pancreas and evaluated growth kinetics. The strength of this study in part comes from their use of extensive clinical data from 101 patients who underwent autopsy, and 127 patients treated with curative surgical resection followed by adjuvant therapy. Overall survival in the autopsy group was a median of 11.4mo and 21.0mo in the adjuvant group. The tumor kinetic data was developed using their model with data from the autopsy group and then validated using data from the adjuvant group.
The investigators review findings which support the notion that metastasis is a late event in the clonal evolution of pancreatic cancer [7]. By using data from patients who died of pancreatic cancer, with tumors measured at multiple time points, the study shows that an exponential growth model more accurately fits (median R2=0.63) the clinical growth pattern than a linear growth model. The model starts with a single cell that is not able to metastasize (type-0 cell), which the multiplies exponentially and gains the ability to metastasize (type-2 cell). They assume that a single genetic alteration is sufficient to confer metastatic ability to pancreatic cancer cells. These cells then metastasize at a certain rate at distant sites. The total number of cells is designated as M1. The mathematical model then allows four possible options at this point including no treatment, surgical resection of the primary tumor, systemic therapy, or surgery plus systemic therapy. The authors studied tumor size and growth kinetics and found that a consideration of both parameters offers an opportunity to optimize the timing of therapy. This result of this study using a complex mathematical model supports the notion that most patients harbor metastatic disease at the time of diagnosis [7]. This may not be a surprise to clinicians who treat this disease on a regular basis, but the fact that the outcome of the model predicts what we know clinically is extremely promising for future development of more sophisticated computational models. The strength of this approach is that it is based in well-annotated data derived from large series of patients. The greatest implication of this model is that it predicts optimal timing and type of intervention impacts survival [7].
The application of analytic techniques from the physical sciences and mathematics to the problems of clinical oncology has just begun. Data based on the mathematical modeling of pancreatic cancer is enticing, and may offer important insights into optimal clinical management. Many readers of the Journal of the Pancreas will not undertake research in this exciting field, yet without the insight of experienced clinicians, those who do this research may “miss the mark”. Success in this burgeoning field will require the close cooperation of physical scientists and seasoned clinicians in the coming years.
Authors declare to have no conflict of interest.