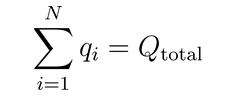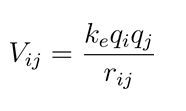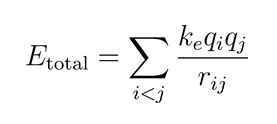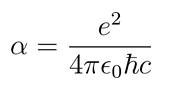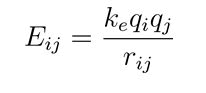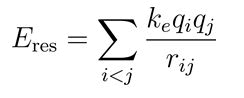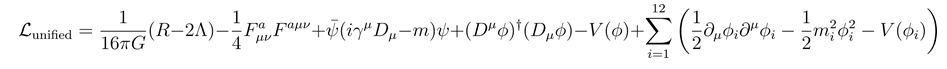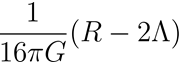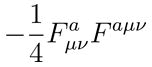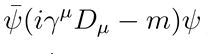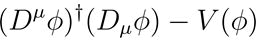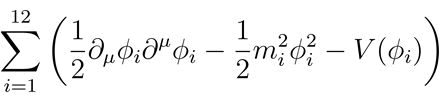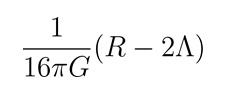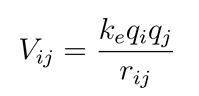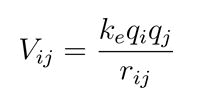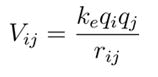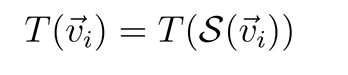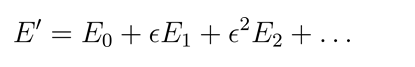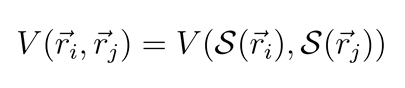Review Article - (2025) Volume 12, Issue 1
Received: 12-Jul-2024, Manuscript No. IPBJR-24-20771; Editor assigned: 16-Jul-2024, Pre QC No. IPBJR-24-20771 (PQ); Reviewed: 30-Jul-2024, QC No. IPBJR-24-20771; Revised: 12-Jan-2025, Manuscript No. IPBJR-24-20771 (R); Published: 19-Jan-2025, DOI: 10.35841/2394-3718-12.1.116
The Dodecahedron Linear String Field Hypothesis (DLSFH) provides a novel theoretical framework that integrates string theory, quantum field theory and general relativity into a unified field theory. This model explains why gravity might not be inherently quantum. Unlike traditional approaches that aim to quantize gravity, the DLSFH maintains the classical description of gravity while incorporating gravitational interactions within the broader framework of unified field theory. This paper explores the key components of the DLSFH, its mathematical formulations and the implications of a nonquantum gravitational theory.
Quantum entanglement; Superposition principle; Rotation operators; Trigonometric identities; Quantum mechanics; Time
The quest for a Unified Field Theory (UFT) has been a central goal in theoretical physics, aiming to reconcile the four fundamental forces of nature gravity, electromagnetism, the weak nuclear force and the strong nuclear force within a single cohesive framework. The DLSFH presents a novel approach by integrating string theory, quantum field theory and general relativity into a unified model that addresses the fundamental interactions of particles and fields without necessitating a quantum description of gravity [1].
Model Structure and Symmetry
The DLSFH model is built on the foundation of dodecahedral symmetry, where each quark is represented by a specific configuration of 12 string qubits distributed across 20 vertices and interacting along 30 edges. This geometric structure ensures the preservation of symmetry and stability within particle configurations.
Dodecahedral symmetry: The dodecahedron, with its 12 faces, 20 vertices and 30 edges, provides a symmetrical framework for string interactions. Each face is a regular pentagon and each vertex is a convergence point for three faces, ensuring consistent string interactions and charge distributions.
String Configuration and Interaction
Each vertex of the dodecahedron is assigned a specific string qubit, ensuring charge balance and symmetry. This configuration plays a crucial role in maintaining the stability and consistency of particle interactions within the DLSFH framework [2].
Vertex assignment and charge distribution: To ensure charge balance, each string qubit at a vertex of the dodecahedron is assigned a specific charge. The charges are distribute such that the sum of all charges at the vertices maintains overall neutrality or the required net charge for the particle. Mathematically, if represents the number of vertices (which is 20 for a dodecahedron) and represents the charge at vertex, the charge distribution can be expressed as:
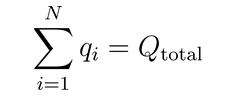
where Qtotal is the net charge of the particle (e.g., for a proton, Qtotal=+1).
Potential energy of string interactions: The interaction between string qubits at vertices and can be described by the potential energy term, which depends on the charges and the distance between the vertices:
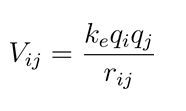
Where is the Coulomb constant.
The total potential energy for a quark configuration can be written as the sum of the interaction energies between all pairs of string qubits:
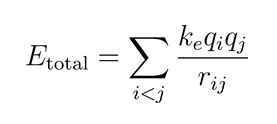
This ensures that the interactions between the strings are accounted for in a manner that maintains the configuration's overall stability and symmetry [3].
Coupling constants and interaction strengths: The coupling constant α for the interaction between strings is given by:
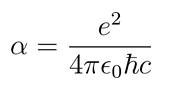
Where is the elementary charge, ϵ0 is the permittivity of free space, ħ is the reduced Planck's constant and is the speed of light. This constant plays a crucial role in determining the strength of the interactions between string qubits.
String dynamics and resonance energies: The resonance energy calculations for string pairs within the dodecahedral structure can be described using the potential energy formula. For string pairs with charges and the resonance energy is:
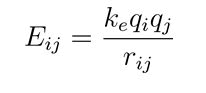
The total resonance energy for the system is the sum of all individual resonance energies:
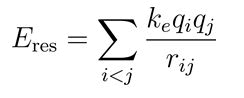
Stability of the configuration: To ensure the stability of the quark configurations, the interaction terms must be balanced such that the total energy remains at a minimum. This balance is achieved through the precise distribution of charges and distances between vertices, guided by the principles of dodecahedral symmetry [4].
Mathematical Framework for Non-Quantum Gravity
Unified Lagrangian density: The unified Lagrangian density is at the heart of the Dodecahedron Linear String Field Hypothesis (DLSFH). This density captures the essential elements of gravitational, gauge, fermion, Higgs and string dynamics, unifying them into a single cohesive framework. The Lagrangian is expressed as:
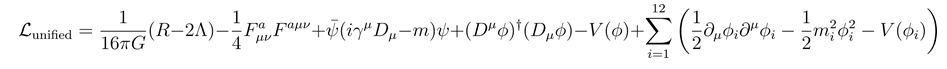
This equation brings together various terms representing different forces and particles:
Gravitational term
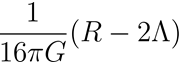
incorporates the curvature of spacetime and cosmological constant.
Gauge field term
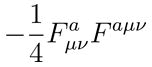
represents the dynamics of the gauge fields.
Fermion field term
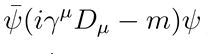
accounts for the behavior of fermions.
Higgs field term
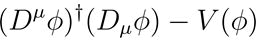
describes the Higgs mechanism.
String dynamics term
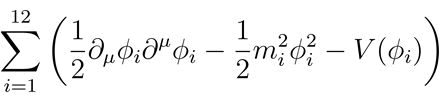
details the dynamics of the string qubits.
Incorporation of General Relativity
The DLSFH seamlessly incorporates general relativity at low energy scales by including the Einstein-Hilbert action within the unified Lagrangian. This ensures that gravitational interactions are described accurately according to general relativity principles. Specifically, the term
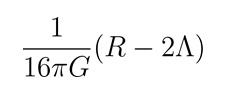
Represents the curvature of spacetime (encoded in the Ricci scalar and the cosmological constant Λ, ensuring that the classical description of gravity holds at macroscopic scales.
String Dynamics and Gravitational Interactions
In the DLSFH, gravitational interactions are treated within the context of string dynamics. The graviton, which mediates gravitational force, is modeled as a vibrational mode of the string. This interaction is captured by the coupling between the string field's energy-momentum tensor and the spacetime curvature. This innovative approach allows gravity to be incorporated without requiring a separate quantum field theory for gravity [5].
Mathematical Recommendations
Numerical simulations and high-performance computing: Numerical simulations are crucial for exploring the Dodecahedron Linear String Field Hypothesis (DLSFH). Computer models allow us to delve into the complex interactions of string qubits within a dodecahedron, helping us understand the system's stability and behavior [6].
Modeling string interactions: Simulations can recreate interactions between string qubits at the vertices of a dodecahedron. Each string qubit has a specific charge and mass, and the computer models calculate the potential energy between them using the formula:
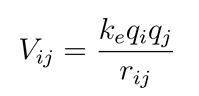
Here are the charges, is the distance between the vertices, and is a constant. By dynamically updating these interactions, we can see how the system evolves over time.
Stability analysis: Simulations allow us to check if the dodecahedral configuration is stable. By simulating the system under various conditions, we can observe how it behaves over time. If the string qubits return to their original positions after being slightly disturbed, the configuration is stable. If they don't, it might be unstable.
Dynamic behavior: Simulations let us see the system's dynamic behavior in real time. We can watch how string qubits interact and move, witnessing phenomena like resonance and energy transfer. This behavior gives us a clearer picture of how the system works and how the interactions unfold [7].
Visualization of complex interactions: Using advanced tools, we can create graphical representations of the string qubits and their interactions. These visualizations help us understand the underlying physics and communicate our findings.
Validation of theoretical predictions: Simulations are essential for testing the accuracy of the DLSFH's predictions. We can see if they match by comparing simulation results with theoretical predictions. For example, if simulations show the expected modifications in gravitational forces at small scales, it supports the hypothesis.
Exploring parameter space: Simulations allow us to explore a wide range of parameters, such as different charge distributions and masses of string qubits. By systematically varying these parameters, we can identify the conditions under which the dodecahedral structure is stable or unstable. This helps us understand the critical factors that influence the system's behavior.
High-performance computing: Given the complexity of these simulations, we need high-performance computing resources. Using powerful computers with parallel processing capabilities, we can perform large-scale simulations that provide detailed and accurate results, enhancing our understanding of the DLSFH [8].
Integration with experimental data: Simulations can be integrated with experimental data to refine the DLSFH. By comparing simulation outcomes with data from precise gravitational measurements and gravitational wave observations, we can adjust our model to match reality better. This iterative process helps us improve the hypothesis.
Analytical Solutions
Specific scenarios and mathematical formulation: Deriving exact mathematical solutions for specific scenarios within the DLSFH is essential for validating and deepening our understanding of this theoretical framework. These solutions help us gain precise insights into the configurations and interactions of quarks within particles like protons and neutrons.
Specific scenarios: We focus on scenarios such as the configurations of quarks within protons and neutrons. Protons consist of two up quarks and one down quark (uud), while neutrons are made up of two down quarks and one up quark (udd). Each quark can be represented by a unique arrangement of string qubits within the dodecahedral framework.
Mathematical formulation: For each quark configuration, we derive the exact mathematical expressions describing the system. This involves calculating the potential energy, kinetic energy and overall stability of the quarks. The potential energy between two quarks and at vertices.
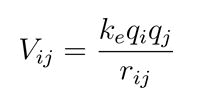
Here are the charges of the quarks, is the distance between the vertices and is the Coulomb constant. The total potential energy for the system is the sum of all pairwise interactions.
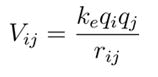
Quark Configurations in Protons and Neutrons
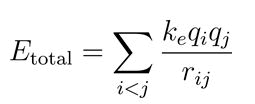
For a proton (uud), we assign the charges qu=+2e/3 for up quarks and qd=-1e/3 for the down quarks. The potential energy contributions for a proton can be calculated as follows:
Similarly, for a neutron (udd), the charges are assigned and the potential energy is calculated accordingly:
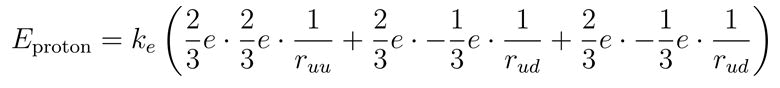
Validation of Fundamental Principles and Deeper Understanding
Validation of fundamental principles: By deriving these exact solutions, we can validate the DLSFH's fundamental principles. For instance, if the derived energies match the experimentally observed values for protons and neutrons, this supports the hypothesis that the dodecahedral string framework accurately describes quark configurations [9].
Deeper understanding: Analytical solutions provide a deeper understanding of the system's behavior under various conditions. By analyzing how the potential energy changes with different quark separations or charge distributions, we can gain insights into the forces that hold the particles together and the stability of the configurations.
Symmetry and stability: Analytical solutions are vital for exploring the symmetry properties of the dodecahedral structure. Ensuring that these solutions respect the dodecahedral's symmetry operations helps confirm the model's consistency and stability. This involves checking that the potential and kinetic energies remain invariant under symmetry transformations. If represents the potential energy between vertices, applying a symmetry operation should not alter this energy:
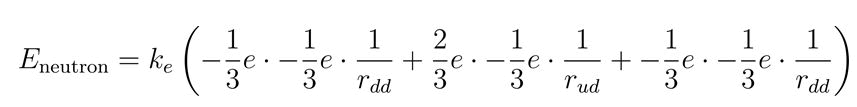
Similarly, the kinetic energy of a qubit with velocity shoul d remain the same under a symmetry transformation.
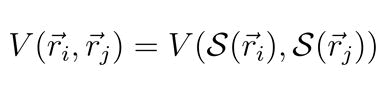
This analysis helps ensure that the system's energy landscape is smooth and consistent, free from irregularities that could cause instability.
Implications of Non-Quantum Gravity
Consistency with observations: The Dodecahedron Linear String Field Hypothesis (DLSFH) preserves the classical description of gravity as outlined by Einstein's general relativity. This approach is well-aligned with current observational data and experimental results. For instance, general relativity has been confirmed through numerous experiments, such as the perihelion precession of Mercury, the deflection of light by the Sun and the precise measurements of gravitational waves. By maintaining this classical perspective, the DLSFH provides a robust and coherent alternative to the necessity of quantizing gravity, addressing the macrocosmic phenomena without contradicting established empirical evidence.
Experimental Predictions
The DLSFH not only aligns with existing data but also makes new, testable predictions. These predictions focus on gravitational phenomena, particularly at small scales where deviations from Newtonian gravity might be observed.
High-precision measurements: Experiments could be designed to measure gravitational interactions at very small distances. Using torsion balances, atomic interferometry or laser-based techniques, scientists can achieve the necessary precision to detect any deviations predicted by the DLSFH.
Gravitational wave observations: Gravitational wave observatories provide another avenue for testing the DLSFH. By analyzing data from events such as binary black hole mergers or neutron star collisions, researchers can compare the observed waveforms to the predictions made by the DLSFH. Any discrepancies or unique signatures could offer evidence supporting this hypothesis.
Unified Description of Fundamental Forces
One of the most significant implications of the DLSFH is its ability to integrate gravitational interactions within a unified field theory. By doing so, the DLSFH offers a comprehensive framework that encompasses all fundamental forces gravity, electromagnetism, the weak nuclear force and the strong nuclear force without the need for a separate quantum theory of gravity. This unification is achieved through the incorporation of string dynamics and dodecahedral symmetry, which elegantly ties together the interactions of particles and fields.
Theoretical integration: The theoretical integration provided by the Dodecahedron Linear String Field Hypothesis (DLSFH) offers a simpler and more cohesive way to understand the universe's fundamental interactions. By treating gravity as a classical force within this unified model, the DLSFH sidesteps the complexities and inconsistencies that often arise when trying to quantize gravity on its own.
Simplifying fundamental interactions: The DLSFH unifies the four fundamental forces gravity, electromagnetism, the weak nuclear force, and the strong nuclear force into a single elegant framework. By incorporating gravity as a classical force, we avoid the challenging and sometimes contradictory efforts to create a quantum theory of gravity, which has yet to be fully realized.
Perturbation theory: To ensure the DLSFH model is robust and stable under various conditions, we apply perturbation theory. This mathematical tool helps us understand the effects of small deviations from the ideal dodecahedral configuration. For example, if a string qubit's ideal position is, a perturbed position might be:
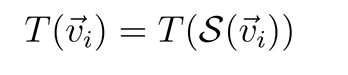
Here, represents a small deviation and is a small parameter. Perturbation theory helps us calculate how these small deviations affect the potential energy of the system. If the potential energy in the ideal configuration is E0, the energy with the perturbations added can be expressed as:
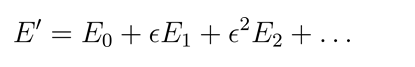
By analyzing these corrections, we can determine if the system remains stable or becomes unstable under small perturbations.
Group theory analysis: Group theory is another crucial tool for ensuring the theoretical integrity of the DLSFH. This branch of mathematics helps us analyze the symmetries of the dodecahedron and ensure that all symmetry operations are accurately reflected in the model. For the dodecahedron, these elements are the symmetry operations (rotations and reflections) that map the shape onto itself. By using group theory, we can:
Identify symmetry operations: Clearly define the 60 symmetry operations of the dodecahedral group.
Incorporate symmetry constraints: Ensure our mathematical equations and solutions respect these symmetry operations, keeping the system's behavior unchanged.
Check invariance: Verify that potential and kinetic energies remain invariant under these operations.
We use symmetry matrices to represent the rotational and reflection operations. For example, a 120-degree rotation around a specific axis can be represented by a matrix R. Applying these matrices to the position and velocity vectors of the string qubits helps us check for invariance. If is the potential energy between vertices applying a symmetry operation S should leave it unchanged:
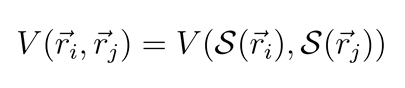
This invariance ensures that the overall potential energy is symmetrical and stable.
By combining perturbation theory and group theory, we can thoroughly analyze the DLSFH model, ensuring it is both robust and consistent. These mathematical tools help us understand how small changes and symmetries impact the model, ultimately leading to a more comprehensive and reliable unified theory of fundamental interactions.
The Dodecahedron Linear String Field Hypothesis (DLSFH) represents a significant step forward in the quest for a unified field theory.
By maintaining a classical description of gravity while integrating it within a unified model of fundamental interactions, the DLSFH offers a compelling framework that challenges the conventional necessity of quantizing gravity.
This model not only advances our understanding of fundamental interactions but also opens new avenues for theoretical exploration and empirical validation.
Further research can look at the sustainability of this festival and its impact on social development and the environment. In this way, researchers can gain a better understanding of the environmental impact and the economic benefits of events. It also enables researchers to develop strategies to ensure the festival’s long-term success and positive contribution to the community and environment. In addition, further studies can also focus on the critical successful factors of a sustainable sky lantern festival, striving to plan strategies regarding a profitable and sustainable festival event.
Citation: Valamontes A (2025) The Dodecahedron Linear String Field Hypothesis (DLSFH): A Framework for Non-Quantum Gravity. Br J Res. 12:116.
Copyright: © 2025 Valamontes A. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
