Short Communication - (2015) Volume 1, Issue 1
Gary Goldstein1*, Yash Kapadia2, Terry Y Lin1 and Paul Zhivago1
Department of Prosthodontics, New York University College of Dentistry, New York, USA
Former Resident Advanced Education Program in Prosthodontics, New York University College of Dentistry, New York, USA
*Corresponding Author:
Gary Goldstein
Department of Prosthodontics
New York University College of Dentistry, 308 Second Ave
NY 10010, New York
USA
E-mail: gary.goldstein@nyu.edu
Received date:: November 09, 2015; Accepted date:: November 17, 2015; Published date:: November 20, 2015
Citation: Goldstein G The Catenary Curve: A Guide to Mandibular Arch Form. Periodon Prosthodon 2015, 1: 1.
This article revisits a pre-existing geometric concept, the catenary curve, redefines its dental application and proposes it as a useful aid in visualizing the mandibular dental arch form both clinically and in CADCAM design.
Keywords
Catenary curve; Parabolic curve; CAD-CAM; Artificial tooth placement; Mandibular arch form
Introduction
The Miriam Webster online dictionary describes the catenary curve as: “the curve assumed by a cord of uniform density and cross-section that is perfectly flexible but not capable of being stretched and that hangs freely from two fixed points”. It was first described by MacConaill and Scher [1], who suggested that normal human dental arches conform closely to a catenary curve. Scott [2], in a paper using a catenometer on dried skulls, concluded that the lower border of the mandible more closely follows a catenary curve rather than the dental arches. Currier’s [3] study on the radiographs of 25 dental cast showed that the ellipse showed a smaller variation than the parabola when using the facial surfaces of the maxillary teeth, while results were reversed in the mandible. Musich and Ackerman [4], in a study of 20 mandibular casts using the mesial of the mandibular first molar as the posterior hanging points, found the catenary method more reliable than the brass wire method when estimating the available arch perimeter. Pepe [5] used complex mathematical formulae to delineate the maxillary and mandibular arch forms of seven children and found that the defining anatomic tooth landmarks were inaccurate. Rudge [6], in a narrative review in 1982, advised caution “when treating individuals to a mathematically derived ideal and when making arch wires to specific “ideal” shapes”. Battagel [7] evaluated the study casts of 35 children utilizing distal molar contacts and found that while the catenary curve approximated the arch forms reliably, it did not work well on square arches. Treviño [8] used glass beads attached to the buccal surfaces of mandibular teeth on 63 adolescents to estimate where the arch wires should be and found different forms; while the authors concluded that there was no representative form, their Figure 2, showing the graphic representation of the hundred and 26 curve elements appears catenary. Sicher and DuBrul [9] described the mandibular arch as parabolic and Stanton found that 25% of the arches he studied were parabolic. Merriam-Webster defines the parabola as: “a plane curve generated by a point moving so that its distance from a fixed point is equal to its distance from a fixed line: the intersection of a right circular cone with a plane parallel to an element of the cone.”
Although most previous studies were performed by orthodontists with the intent of designing arch wires, dental arch forms are undoubtedly just as important to prosthodontists. The orthodontic literature focused on the first molars as the fixed point, which is problematic for the restorative dentist as they are rarely in an ideal position and usually missing or in need of a restoration. The retromolar pad, a commonly used, relatively stable anatomic landmark is proposed as an optimal choice. Having three points to work with, the two fixed posterior “hang points” and the incisal edges of the mandibular central incisors, allows the visualization of the mandibular arch form which falls into a symmetric curve. As shown in Figure 1 (an intact dentition) and 2 (an artificial dentition), the parabolic curve, when superimposed on the mandibular teeth, does not fit as well as the catenary curve if one utilizes the buccal cusps of the mandibular posterior teeth as a guide. What can be debated is that since the mid-retro molar pad is the suggested posterior “hang point”, and having the central fossae of the posterior teeth over the crest of the ridge is an oft used anatomic landmark, then perhaps the parabolic curve would be more useful is planning the initial artificial tooth placement?
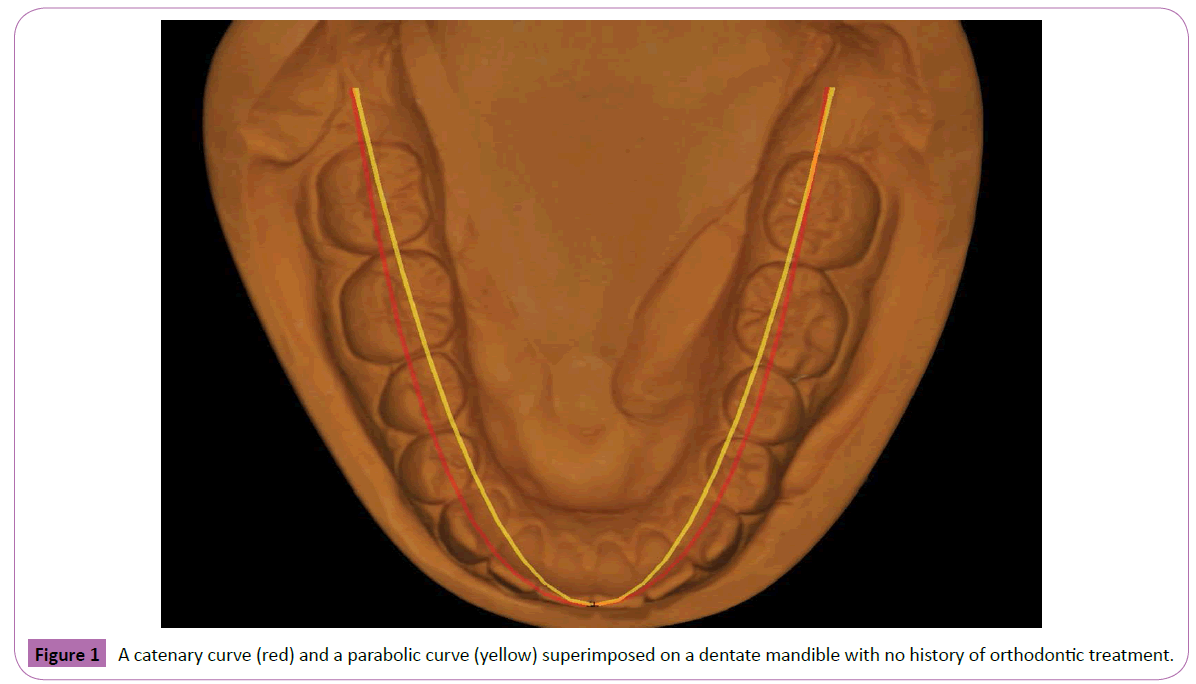
Figure 1: A catenary curve (red) and a parabolic curve (yellow) superimposed on a dentate mandible with no history of orthodontic treatment.
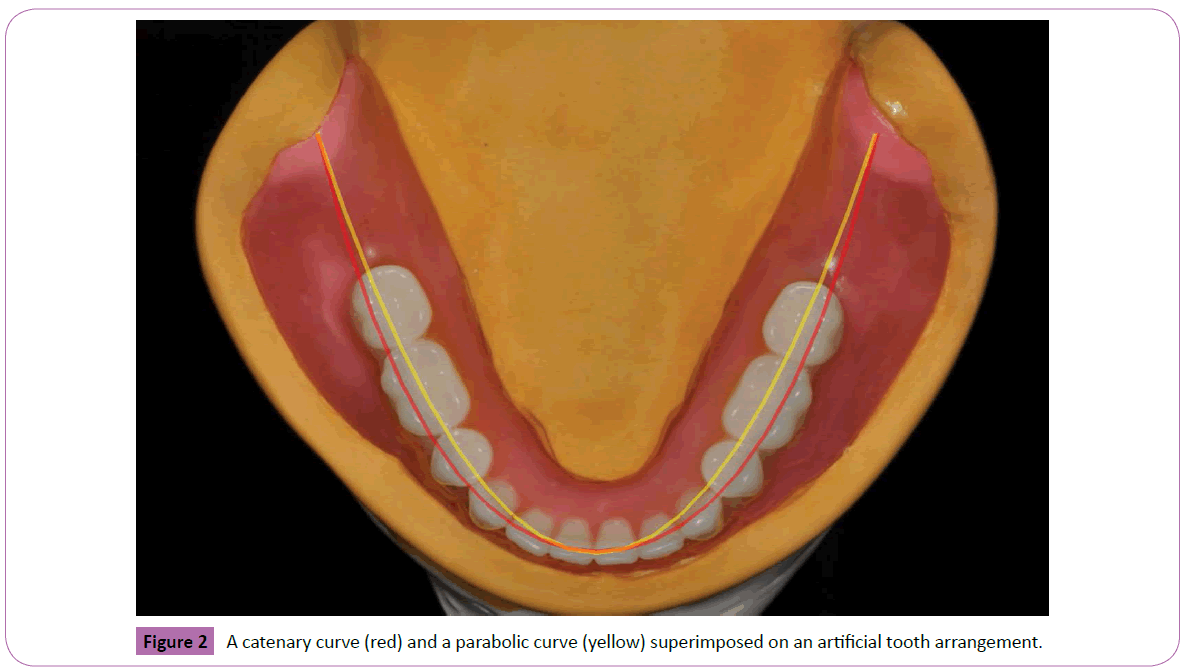
Figure 2: A catenary curve (red) and a parabolic curve (yellow) superimposed on an artificial tooth arrangement.
What is unarguable is that all of the buccal cusps of the natural teeth will not rest on the curve and individual anatomic variations, seen in the general population; show that it can only be used as a visual guide and not as a rule. Asymmetry is prevalent in the natural dentition, but not so much in the restored dentition where aesthetics and occlusal design often require bilateral symmetry.
Summary
The catenary curve, using the retro molar pad and the proposed or actual tips of the mandibular central incisors, can be utilized as a visual restorative guide for the initial placement and arrangement of artificial teeth, in conjunction with a removable or fixed (tooth or implant supported) prosthesis. It is especially helpful when utilizing CAD-CAM technology. What is obvious is that the tapered arch will be more parabolic and the square arch will be neither. The ultimate position of the teeth would be finalized when coordinating the anatomical, functional and aesthetic requirements of the individual patient.
