Research Article - (2011) Volume 1, Issue 4
1Department of Economics, University of Qom, Iran
2Department of Economics, Babol Branch, Islamic Azad University, Babol, Iran
The main objectives of macroeconomic policies, in general, and monetary policies, in particular, are price stability, economic growth and a favorable employment level. This article estimates the major determinants of monetary Policy and investigates how effects of monetary Policy have changed industry sector Growth in Iran. The theoretical framework is based on this assumption that the real output is inversely related to the interest rate but it is shifted by monetary policy. This study uses annual time series data (1961-2007) and unit root tests and analyze them using Auto Regressive Distributed Lag (ARDL) model by Pesaran et al. [1]. This co-integration technique accommodates potential structural breaks that could undermine the existence of a long-run relationship between monetary Policy and industry sector Growth and its main determinants.
Industry sector Growth, monetary Policy, unit root test, autoregressive distributed lag (ARDL).
In the literature, macroeconomists have established the theoretical relationship between real output and monetary policy measures. To Keynesians, a discretionary change in money supply permanently influences real output by lowering the rate of interest and through the marginal efficiency of capital, stimulate investment and output growth [2,3]. In contrast to Keynesian policy prescription, McKinnon [4] and Shaw [5] in advocating the financial liberalization hypothesis argued that a market force induced higher interest rate, would enhance more investment by channeling saving to productive investment and stimulate real output growth.
Based on these theoretical propositions, empirical questions have been raised on whether this consensus views on the effect of monetary policy on the real output holds for the different sectors of the economy. Existing studies have shown that the effects of monetary policy on sectors output varies and such variation might arise because of the relative strength of a particular channel of monetary of transmission mechanism on some sectors than for sectors [6]. Also, the possibility of a differential response between sect oral output and aggregate output to monetary policy measures has been investigated by Granley and Salmon [7] for other countries. In many regards, the recent history of monetary economics can be understood as exploring different elements of the monetary authority’s constrained maximization program. In the early 1970s debate focused on the “instrument choice” question, and whether monetary policy should target the interest rate or money supply. Poole [8] examined this question within the context of the neo-Keynesian ISLM model. Sargent and Wallace [9] examined it using a new classical rational expectations (RE) model. Post-Keynesians, with their theory of endogenous money supply [10] have criticized this debate arguing that money supply targeting is infeasible because the money supply is determined by bank lending. That means the monetary authority can only target the interest rate.
The mid-1970s and early 1980s saw a dramatic change in the framing of the optimal monetary policy problem. Lucas [11] adopted a classical macroeconomic framework with rational expectations (RE), and argued that “fooling” workers about inflation explains why output and employment respond positively to inflation. His work triggered a two-fold shift. First, and most importantly, there was a shift from using Keynesian economics to describe the structure of the economy to using classical macroeconomics. Second, RE shifted attention to issues of the distribution of information about inflation, learning and agents’ responses to monetary policy [11]. Thus, the effectiveness and impact of policy could change as agents learned and responded. Concern with learning and response then directed attention toward time and game theoretic considerations. Kydland and Prescott [12] introduced the time-consistency problem for monetary policy, while Barro and Gordon [13] introduced gaming between the monetary and economic agents. These concerns in turn triggered interest in issues of policy credibility, giving rise to the “rules vs. discretion” policy literature [14]. Additionally, these models tacitly smuggled in the assumption that the monetary authority’s social welfare function was different from the public’s welfare function, which contrasts with the Keynesian literature that assumed a benevolent policy maker [15].
Monetary Policy in Islamic Republic of Iran
After the Islamic revolution in Iran, at 1979, there were comprehensive attempts by government to use Islamic rules and regulations in all aspects of society and economic and banking system of the country was one these aspects. Finally at 1983 economic experts and Shariah scholars provided the Interest Free Banking System Bill to the parliament that used Islamic contracts as instruments for attracting and allocating money in the banking system. After approving process by parliament, and Guardian Council, which contains 6 lawyers and 6 Islamic jurists who monitor all parliament approvals not to be against Islamic rules, from the 1984, the whole economic and banking system of country changed to Islamic one. Unlike some Islamic countries which have both Islamic and non-Islamic banking system, there is not any bank in Iran that works according to interest rate system. From the beginning of the Islamic banking system, the central bank of Iran did its best to use monetary policy instruments which have no contradiction to Islamic rules and at the same time bring macroeconomic stability and growth to the country. We can see that Central Bank of Iran does not restrict itself only to monetary aggregate instrument of monetary policy and uses extensively from profit rate instrument like Musharakah certificates. Here, we explain the instruments that central bank currently uses to execute monetary policy1.
Monetary Policy Instruments in Iran2
In implementing monetary policy, the Central Bank can directly resort to its regulating power or affect money market conditions indirectly as issuer of high-powered money (notes and coins in circulation and deposits held with Central Bank). On this basis, two different monetary policy instruments are being utilized: direct instruments (with no reliance on market conditions) and indirect instruments (market-oriented).
Direct Instruments
With the implementation of Usury-free Banking Law and the introduction of contracts with fixed return and partnership contracts, the regulations pertaining to determination of profit rate or expected rate of return on banking facilities and the minimum and maximum profit rate or expected rate of return, as is stipulated in the by-law of the Usury free Banking Law, are determined by the Money and Credit Council (MCC). Moreover, the Central Bank of Iran (CBI) can intervene in determining these rates both for investment projects or partnership and for other facilities extended by banks. According to Article 14 of the Monetary and Banking Law of Iran, the CBI can intervene in and supervise monetary and banking affairs through limiting banks, specifying the mechanisms for use of funds and determining the ceiling of loans and credits in each sector.
Indirect Instruments
Reserve Requirement Ratio (RRR) is one of the CBI’s indirect instruments of monetary policy. Banks are obliged to deposit part of their liabilities in the form of deposit with the CBI. Through increasing/decreasing this ratio, the CBI contracts/expands the broad money. According to Article 14 of the Monetary and Banking Law of Iran, the CBI is authorized to determine RRR within 10 to 30 percent depending on banks’ liabilities’ composition and field of activity. Appropriate implementation of monetary policies by the CBI is done through open market operations, which provide the required flexibility in liquidity management and intervention in the money market. Following the implementation of the Usury free Banking Law, tailoring appropriate Sharia-based instruments for the development of open market operations in the context of liquidity management and affecting money and capital market became a necessity. Utilization of bonds, owing to its fixed interest rate nature, is prohibited according to Islamic Sharia; however, utilization of participation papers and investors’ partnership in economic activities and payment of profit is encouraged. According to the 3rd FYDP3 Law, the CBI was authorized to issue participation papers through the MCC approval. However, based on the 4th FYDP Law, issuance of Participation Papers by the CBI is authorized upon the approval of the Parliament. By using this instrument, the CBI could affect broad money (M2) through monetary base, thereby controlling the rate of inflation. One of the bold measures taken for the efficient utilization of indirect monetary instruments in the framework of the Usury-free Banking Law is to allow banks to open a special deposit account with the CBI. Regulation on ODA was approved by the MCC at the end of 1998-99. The main objective of this plan was the adoption of appropriate monetary policies to control liquidity through absorption of banks’ excess resources. The CBI pays profit to these deposits on the basis of specific rules.
The present research explores from macro perspective an alternative way in which the industry sector growth could be explored employing time series data. Following Bernanke and Blinder [16], the real output is inversely related to the interest rate but it is shifted by monetary policy, R, and by credit shock that affected either the loans demand or supply functions [17]. For that purpose, we use the bounds testing (or ARDL) approach to co-integration proposed by Pesaran et al. [1] to test the effects of monetary Policy on industry sector growth in Iran using data over the period 1961–2007. The ARDL approach to co-integration has some econometric advantages which are outlined briefly in the following section. Finally, we apply it taking as a benchmark Bernanke and Blinder [16] study in order to sort out whether the results reported there reflect a spurious correlation or a genuine relationship between on industry sector growth and the variables in question. This contributes to a new methodology in the on industry sector growth literature. Next section starts with discussing the model and the methodology. Then in Section 3 we describe the empirical results of unit root tests, the F test, ARDL co-integration analysis, Diagnostic and stability tests and Dynamic forecasts for dependent variable and Section 4 summarizes the results and conclusions.
The model
Following the practice in the literature, the loan rate that cleared the loan market can be stated:

Equation (1) showed that the interest rate on loans was positively related to interest rate on bonds and income, but inversely related to bank reserves. To solve for the aggregate demand curve; Bernanke and Blinder [16] used the following generic IS curve:

And then by substituting equation (1) into (2), we have:

As expressed by Bernanke and Blinder [16] the real output is inversely related to the interest rate but it is shifted by monetary policy, R, and by credit shock that affected either the loans demand or supply functions [17]. By expressing equation (3) in more explicit forms and accommodating other relevant variables in the model, equation (3) can be expressed as a simple linear equation model is summarized as:
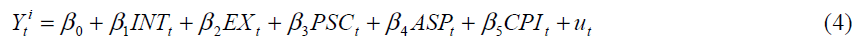
Where: Y= real output, INT= interest rate, EX= exchange rate, PSC = credit to the private sector, ASP = all share price index, CPI = consumer price index Equation (4) was the baseline model for the analysis of the effects of monetary policy on each of the sect oral outputs. The following modified model in logarithm form is used to examine the monetary policies in industry sector in Iran. The logarithm equation corresponding to Eq. (4) and breakdown of the factors industry sector gives:
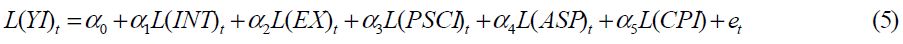
Where YI is real output in industry sector and PSCI is credit to the private sector in industry. Our empirical analysis in Section 3 is based on estimating directly long-run and short-run variants of Eq. (5). All the data in this study are obtained from Central Bank of Iran (2004)1 during the period 1961-2007.
The methodology
Recent advances in econometric literature dictate that the long run relation in Eq. (5) should incorporate the short-run dynamic adjustment process. It is possible to achieve this aim by expressing Eq. (5) in an error correction model as suggested by Engle and Granger [18]. Then, the equation becomes as follows:
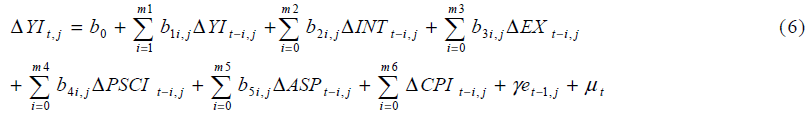
Where Δ represents change, mi is the number of lags, γ is the speed of adjustment parameter and εt−1 is the one period lagged error correction term, which is estimated from the residuals of Eq. (5). The Engle–Granger [18] method requires all variables in Eq. (5) are integrated of order one, I (1) and the error term is integrated order of zero, I (0) for establishing a co-integration relationship. If some variables in Eq. (5) are non-stationary we may use a new co-integration method proposed by Pesaran et al. [1]. This approach is also known as Auto Regressive Distributed Lag (ARDL) that combines Engle and Granger [18] two steps into one by replacing εt−1 in Eq. (6) with its equivalent from Eq. (5). εt−1 is substituted by linear combination of the lagged variables as in Eq. (7).
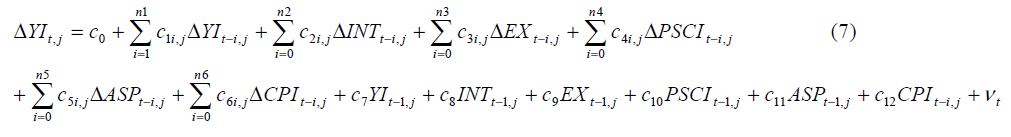
To obtain Eq. (7), one has to solve Eq. (5) for εt and lag the solution equation by one period. Then this solution is substituted for εt−1 in Eq. (6) to arrive at Eq. (7). Eq. (7) is a representation of the ARDL approach to co-integration. Pesaran et al. [1] co-integration approach, also known as bounds testing, has some methodological advantages in comparison to other single cointegration procedures. Reasons for the ARDL are: i) endogenous problems and inability to test hypotheses on the estimated coefficients in the long-run associated with the Engle and Granger [18] method are avoided; ii) the long and short-run coefficients of the model in question are estimated simultaneously; iii) the ARDL approach to testing for the existence of a long-run relationship between the variables in levels is applicable irrespective of whether the underlying regresses are purely stationary I(0), purely non-stationary I(1), or mutually co-integrated, and iv) the small sample properties of the bounds testing approach are far superior to that of multivariate co-integration, as argued in Narayan [19]. The procedure is no longer valid in presence of I (2) series (integrated of order 2). Given that Pesaran et al. [1] co-integration approach is a relatively recent development in the econometric time series literature, a brief outline of this procedure is presented as follows. The ARDL approach involves two steps for estimating the long-run relationship. The bound testing procedure is based on F-statistics and is the first step of the ARDL co-integration method. Accordingly, a joint significance test that implies no cointegration under the null hypothesis, (H0: c4=c5=c6=0), against the alternative hypothesis, (H1: at least one c4 to c6≠0) should be performed for Eq. (7). The F test used for this procedure has a non-standard distribution. Thus, Pesaran et al. [1] computed two sets of asymptotic critical values for testing co-integration for a given significance level with and without a time trend. One set assumes that all variables are I (0) and the other set assumes they are all I (1). If the computed F-statistic exceeds the upper bound critical value, then the null hypothesis of no co-integration can be rejected. Conversely, if the F-statistic falls below the lower bound critical value, the null hypothesis cannot be rejected. Lastly, if the F-statistic falls between these two sets of critical values, the result is inconclusive. The short-run effects between the dependent and independent variables are inferred by the size of coefficients of the differenced variables in Eq. (7). The longrun effect is measured by the estimates of lagged explanatory variables that are normalized on estimate of c4. Once a long-run relationship has been established, Eq. (7) is estimated using an appropriate lag selection criterion. At the second step of the ARDL co-integration procedure, it is also possible to obtain the ARDL representation of the Error Correction Model (ECM). To estimate the speed with which the dependent variable adjusts to independent variables within the bounds testing approach, following Pesaran et al. [1] the lagged level variables in Eq. (7) are replaced by ECt−1 as in Eq. (8):
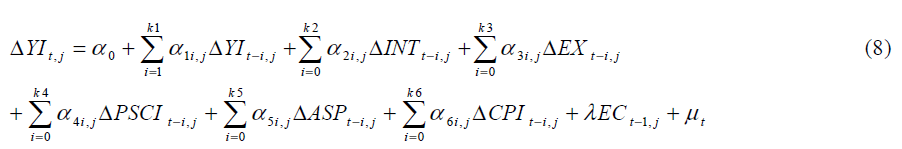
A negative and statistically significant estimation of λ not only represents the speed of adjustment but also provides an alternative means of supporting co-integration between the variables.
Structural stability tests Cumulative Sum (CUSUM) and Cumulative Sum of Square (CUSUMSQ)
There are two statistical methods to test the structural stability of the restricted autoregressive models. These are the cumulative sum and the cumulative sum of squares tests of recursive residuals, which can be shown graphically in the Microfit displays two straight lines that represent the 5 per cent critical bounds where the null hypothesis of having stable parameters for each of the five observed variables is rejected if any of the straight lines is significantly crossed. Otherwise, if the plot generally remains within those two straight lines, the null hypothesis is not rejected. The cumulative sum test helps to show if the coefficient of regression are changing systematically, whereas the cumulative sum of squares test is helpful in showing if the regression coefficients are changing suddenly. These tests have been proposed by Brown et al. [20]. Its foundation is based on that initially, a regression equation including the variable desired is estimated using of estimated to be at least observations. Then, one observation is added to the observations of previous equation and next estimation is performed and in this same way, it is added to the observations a unit. In this way, after the estimation of each step, one coefficient is obtained for any of the variables which finally is concluded a time series of variables coefficients. These tests presents Cumulative sum (CUSUM) and cumulative sum of Square (CUSUMSQ) diagrams between two straight lines (the bounds of the 95 percent).If the diagram presented be within the boundaries, zero hypothesis is accepted which is based on lack of structural break and if the diagram go out of the boundaries (it means that if dealt to them), zero hypothesis is rejected which is based on lack of structural break and the presence of structural break is accepted [21]. CUSUM statistics is useful to find systematic changes in long term coefficients of regression and CUSUMSQ statistics is helpful when deviation from regression coefficients stability is randomized and occasional (short term).
Unit Root Test
We use the Augmented Dickey-Fuller [22] t-statistic when to difference time series data to make it stationary. Here are the various cases of the test equation: A. When the time series is flat (i.e. doesn’t have a trend) and potentially slow-turning around zero, we use the following test equation:
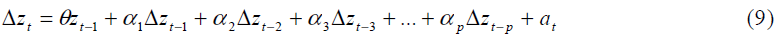
Where the number of augmenting lags (p) is determined by minimizing the Schwartz Bayesian information criterion or minimizing the Akaike information criterion or lags are dropped until the last lag is statistically significant. Mifrofit allows all of these options to choose from. This test equation does not have an intercept term or a time trend. Unfortunately, the Dickey-Fuller tstatistic does not follow a standard t-distribution as the sampling distribution of this test statistic is skewed to the left with a long, left-hand-tail. Microfit will give us the correct critical values for the test, however. Notice that the test is left-tailed. The null hypothesis of the Augmented Dickey-Fuller t-test is:
H0: θ = 0 (i.e. the data needs to be differenced to make it stationary)
Versus the alternative hypothesis of:
H1: θ < 0 (i.e. the data is stationary and doesn’t need to be differenced)
B. When the time series is flat and potentially slow-turning around a non-zero value, we use the following test equation:
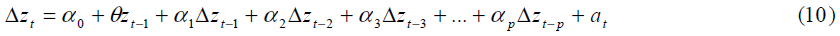
Notice that this equation has an intercept term in it but no time trend. Again, the number of augmenting lags (p) is determined by minimizing the Schwartz Bayesian information criterion or minimizing the Akaike information criterion or lags are dropped until the last lag is statistically significant. Microfit allows all of these options to choose from. We then use the t-statistic on the θ coefficient to test whether we need to difference the data to make it stationary or not. Notice the test is left-tailed. The null hypothesis of the Augmented Dickey-Fuller [22] t-test is:
H0: θ = 0 (i.e. the data needs to be differenced to make it stationary)
Versus the alternative hypothesis of:
H1: θ < 0 (i.e. the data is stationary and doesn’t need to be differenced)
C. When the time series has a trend in it (either up or down) and is potentially slow-turning around a trend line we would draw through the data, use the following test equation:
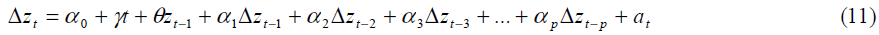
Notice that this equation has an intercept term and a time trend. Again, the number of augmenting lags (p) is determined by minimizing the Schwartz Bayesian information criterion or minimizing the Akaike information criterion or lags are dropped until the last lag is statistically significant. Microfit allows all of these options for us to choose from. We then use the t-statistic on the θ coefficient to test whether we need to difference the data to make it stationary or we need to put a time trend in our regression model to correct for the variables deterministic trend. Notice the test is left-tailed. The null hypothesis of the Augmented Dickey-Fuller [22] t-test is:
H0: θ = 0 (i.e. the data needs to be differenced to make it stationary)
Versus the alternative hypothesis of:
H1: θ < 0 (i.e. the data is trend stationary and needs to be analyzed by means of using a time Trend in the regression model instead of differencing the data)
The results reported in Table 1 show that null hypothesis of ADF unit root is accepted in case of LYI, LEX, LCPI and LPSCI variables but rejected in first difference at 1% level of significance. This unit root test indicate that LYI, LEX, LCPI and LPSCI variables considered in the present study are difference stationary I (1) while LINT and LASP variables are level stationary I(0) as per ADF test. On the basis of this test, it has been inferred that LYI, LEX, LCPI and LPSCI variables are integrated of order one I (1), while LINT and LASP variables are integrated of order zero I (0). Under these circumstances and especially when we are faced with mix results, applying the ARDL model is the efficient way of the determining the long-run relationship among the variable under investigation. Therefore, we will apply this methodology in the section 3.3.
ARDL co-integration analysis for agricultural value added with oil shocks as Structural Breaks: The estimated coefficients of the long-run relationship and Error Correction Mode (ECM) are displayed in Table 2,3. The significance of the Error Correction Term and F-statistics, in Table 2, indicates causal and long term relation among the variables in Iran.
As we see in Table 3, ECM version of this model show that the error correction coefficient which determined speed of adjustment, had expected and significant negative sign. Bannerjee et al. [24] holds that a highly significant error correction term is further proof of the existence of a stable long-term relationship. The results indicated that deviation from the long-term in inequality was corrected by approximately 32 percent over the following year or each year. This means that the adjustment takes place relatively quickly, i.e. the speed of adjustment is relatively high. Also, analyzing the stability of the long-run coefficients together with the short run dynamics, the cumulative sum (CUSUM) and the cumulative sum of squares (CUSUMSQ) are applied. According to Pesaran and Shin [25] the stability of the estimated coefficient of the error correction model should also be empirically investigated. A graphical representation of CUSUM and CUSUMSQ are shown in Figure 1.
Following Bahmani-Oskooee [21] the null hypothesis (i.e. that the regression equation is correctly specified) cannot be rejected if the plot of these statistics remains within the critical bounds of the 5% significance level. As it is clear from Figure 1, the plots of both the CUSUM and the CUSUMSQ are within the boundaries and hence these statistics confirm the stability of the long run coefficients of regressors which affect the inequality in the country. The stability of selected ARDL model specification is evaluated using the cumulative sum (CUSUM) and the cumulative sum of squares (CUSUMSQ) of the recursive residual test for the structural stability (see Brown et al., [20]). The model appears stable and correctly specified given that neither the CUSUM nor the CUSUMSQ test statistics exceed the bounds of the 5 percent level of significance.
Expansionary monetary policy implemented can be affect real economic sector noticeably by reduction in the legal deposit rates or increase in the banks debt to the Central Bank and can be positive effects by increase in the production and employment level and increase in the components of total demand and consequently improvements in public welfare. In this pattern, exchange policies implemented by increase in the nominal exchange rate causes to decrease imports and gross domestic product (GDP). Contrary to expectations, this policy affects on non oil export and increase in the production noticeably. The goal of this paper was to test the existence of long run relationship determinants of monetary policies industry sector in Iran. This objective was aided by the technique of Pesaran et al. [21] approach to co-integration which presents non-spurious estimates. Subsequently, our work provides fresh evidence on the long run relationship between monetary policies industry sector in Iran. Results of this study represent Volume of monetary and exchange policies effectiveness in Iran’s economy. This study showed that output growth in the industry can also be enhanced through successful management of the domestic credit through moderate reduction in the cost of borrowing in the financial market. More so, given the significant contribution of domestic credit in influencing the output growth of industry sector, there is the need for monetary authority to reduce the extent of unproductive credit directed to the public authority. Greater proportion of the aggregate domestic credit should be directed to the private sector at a competitive rate with strict guidelines and monitoring. This guidelines and supervision would prevent diversion of the credits to unproductive usage. Prudent use of the credit would promote investment and consequently output growth across sector of the economy.
1These Instruments are introduced in the website of Central Bank of Iran: www.cbi.ir
2Central Bank of Iran: www.cbi.ir
3Pre-revolution economic plans in Iran include: third plan during 1963-1967, fourth plan during 1968-1972, fifth plan during 1973-1977 and economic plans during war and Islamic revolution during 1978 through 1988 and also economic, social and cultural development plans of Islamic republic of Iran including first plan during 1989-1993, second plan during 1994-1998, third plan during 1999-2004 and fourth plan during 2005-2009.